Chọn B.
Đặt AC = x > 0
Áp dụng định lí côsin trong tam giác ABD ta có
BD2 = 1 + (1 + x) 2 - 2.(1 + x). 1/x
Áp dụng định lí sin trong tam giác BCD ta có
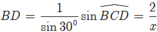
Suy ra ta được phương trình
![]()
Hay ![]() suy ra
suy ra ![]() (do x > 0).
(do x > 0).
Chọn B.
Đặt AC = x > 0
Áp dụng định lí côsin trong tam giác ABD ta có
BD2 = 1 + (1 + x) 2 - 2.(1 + x). 1/x
Áp dụng định lí sin trong tam giác BCD ta có
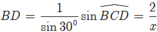
Suy ra ta được phương trình
![]()
Hay ![]() suy ra
suy ra ![]() (do x > 0).
(do x > 0).
cho tam giác ABC vuông tại A (AC>AB) Đường cao AH (H thuộc BC) trên tia HC lấy điểm D sao cho HD=HA . Đường vuông góc với BC tại D cắt AC tại E .
a) CMR hai tam giác BEC và ADC đồng dạng .Tính độ dài BE theo m=AB
b) ọi M là tung điểm của đoạn BE . CMR ha tam giác BHM và BEC đồng dạng . Tính số đo góc AHM
c) Tia AM cắt BC tại G cm \(\dfrac{\text{GB}}{\text{BC}}=\dfrac{\text{HD}}{\text{AH+HC}}\)
Cho tam giác nhọn ABC nội tiếp đường tròn (O) với AB<AC .Đường phân giác của góc B A C ^ cắt (O) tại điểm D khác A
Gọi M là trung điểm của AD và E là điểm đối xứng với D qua tâm O.
Giả sử đường tròn ngoại tiếp tam giác ABM cắt đoạn thẳng AC tại điểm F khácA
2). Chứng minh rằng È vuông góc với AC
Cho tam giác nhọn ABC nội tiếp đường tròn (O) với AB<AC. Đường phân giác của góc B A C ^ cắt (O) tại điểm D khác A
Gọi M là trung điểm của AD và E là điểm đối xứng với D qua tâm O.
Giả sử đường tròn ngoại tiếp tam giác ABM cắt đoạn thẳng AC tại điểm F khácA
1) Chứng minh rằng tam giác ĐM và tam giác BCF đồng dạng.
cho tam giác ABC vuông tại A, AB=3, AC=5. Lấy các điểm M,N trên các cạnh AB,AC sao cho MA=3MB, NC=3NA. đường thẳng qua A vuông góc MN cắt BE tại E. tính EB/EC
Cho tam giác ABC. Trên đoạn BC lấy điểm D sao cho CD=BC/3, trên đoạn AC lấy điểm E sao cho CE=AC/6 . Dựng hình bình hành DCEF. Trên tia FB lấy điểm M sao cho FM=2FB , trên tia FC lấy điểm N sao cho FN=3FC. Chứng minh rằng F là trọng tâm của tam giác AMN.
Cho tam giác ABC, trên các cạnh AB,AC lần lượt lấy D,E sao cho BD = BC = CE. CD giao BE tại F. Chứng minh rằng đường nối tâm nội tiếp I của tam giác ABC với trực tâm H của tam giác DEF đi qua trung điểm cung BAC của (ABC).
Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Gọi M là một điểm trên cạnh BC và D là chân đường phân giác trong góc A. Tính độ dài vecto MD khi độ dài vecto AM nhỏ nhất