\(\text{#TNam}\)
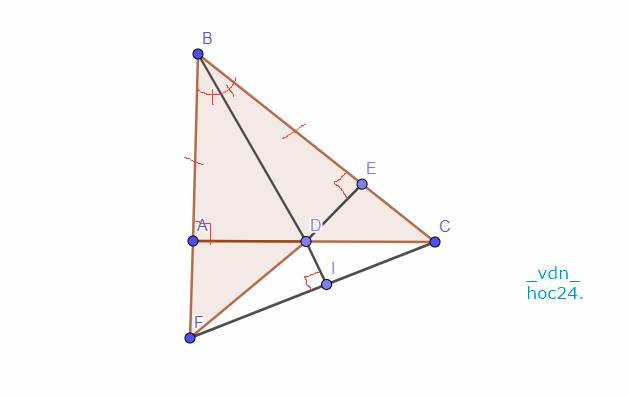
`a,` Xét Tam giác `ABD` và Tam giác `EBD` có:
`\text {BD chung}`
\(\widehat{ABD}=\widehat{EBD} (\text {tia phân giác}\)\(\widehat{BAE})\)
`=> \text {Tam giác ABD = Tam giác EBD (ch-gn)}`
`b,`
Vì Tam giác `ABD =` Tam giác `EBD (a)`
`-> BA = BE (\text {2 cạnh tương ứng})`
Xét Tam giác `BAC` và Tam giác `BEF` có:
\(\widehat{B}\) \(\text {chung}\)
`BA = BE (CMT)`
\(\widehat{BAC}=\widehat{BEF}=90^0\)
`=> \text {Tam giác BAC = Tam giác BEF (g-c-g)}`
`-> BF = BC (\text {2 cạnh tương ứng})`
Gọi `I` là giao điểm của `BD` và `CF`
Xét Tam giác `BIF` và Tam giác `BIC` có:
`BF = BC (CMT)`
\(\widehat{FBI}=\widehat{CBI} (\text {tia phân giác}\) \(\widehat{FBC})\)
\(\text {BI chung}\)
`=> \text {Tam giác BIF = Tam giác BIC (c-g-c)}`
`->`\(\widehat{BIF}=\widehat{BIC} (\text {2 góc tương ứng})\)
Mà `2` gióc này nằm ở vị trí kề bù
`->`\(\widehat{BIF}+\widehat{BIC}=180^0\)
`->`\(\widehat{BIF}=\widehat{BIC}=\)`180/2=90^0`
`-> \text {BI} \bot \text {FC}`
`-> \text {BD}` `\bot` `\text {FC (đpcm)}`