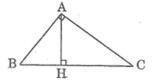
Lời giải:
Vì $AB: AC=3:7$ nên đặt $AB=3a; AC=7a$. Áp dụng hệ thức lượng trong tam giác vuông:
$\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}$
$\frac{1}{42^2}=\frac{1}{(3a)^2}+\frac{1}{(7a)^2}$
$\frac{1}{42^2}=\frac{58}{441a^2}$
$\Rightarrow a=2\sqrt{58}$ (cm)
$AB=3a=6\sqrt{58}$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{(6\sqrt{58})^2-42^2}=18$ (cm)
Chu vi $ABH$: $AB+BH+AH=6\sqrt{58}+18+42=60+6\sqrt{58}$ (cm)
$AC=7a=14\sqrt{58}$ (cm)
$HC=\sqrt{AC^2-AH^2}=\sqrt{(14\sqrt{58})^2-42^2}=98$ (cm)
$S_{AHC}=\frac{AH.HC}{2}=\frac{42.98}{2}=2058$ (cm vuông)