Question

Cho tam giác ABC vuông tại A. Gọi BC = a, AC= b, AB =c. Giải tam giác
ABC, biết.

c) a=15cm, b=10cm.

Answer 1

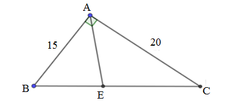
c) Xét \(\triangle ABC\) vuông tại A có: \(a^2=b^2+c^2\) (đli Pythagore)

\(\Rightarrow c^2=a^2-b^2=15^2-10^2=125\\ \Rightarrow c=\sqrt{125}=5\sqrt{5}\left(cm\right)\)

Khi đó: \(\tan B=\dfrac{b}{c}=\dfrac{10}{5\sqrt{5}}\Rightarrow\widehat{B}\approx42^{\circ}\)

\(\Rightarrow\widehat{C}=90^{\circ}-\widehat{B}=90^{\circ}-42^{\circ}=48^{\circ}\)