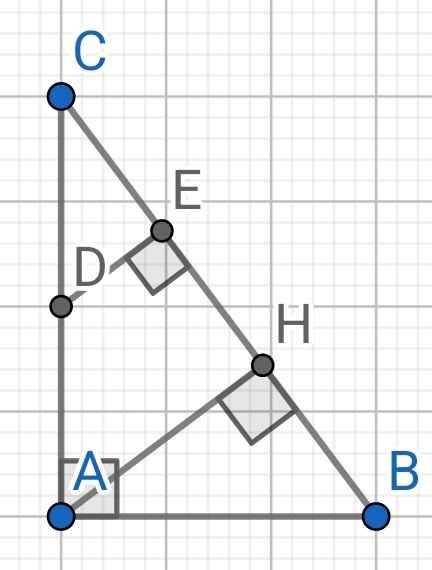
 Do AH là đường cao của ∆ABC
Do AH là đường cao của ∆ABC
⇒ AH ⊥ BC
Mà DE ⊥ BC (gt)
⇒ AH // DE
Lại có DE ⊥ BC (gt)
⇒ ∠DEH = 90⁰
Tứ giác AHED có:
AH // DE (cmt)
⇒ AHED là hình thang
Mà ∠DEH = 90⁰ (cmt)
⇒ AHED là hình thng vuông
 Do AH là đường cao của ∆ABC
Do AH là đường cao của ∆ABC
⇒ AH ⊥ BC
Mà DE ⊥ BC (gt)
⇒ AH // DE
Lại có DE ⊥ BC (gt)
⇒ ∠DEH = 90⁰
Tứ giác AHED có:
AH // DE (cmt)
⇒ AHED là hình thang
Mà ∠DEH = 90⁰ (cmt)
⇒ AHED là hình thng vuông
Cho tam giác ABC vuông tại A, kẻ đường cao AH(H Thuộc BC).Gọi D,E lần lượt là chân đường vuông góc kẻ từ H đến AB,AC.
a) CMR:AH=DE
b) Gọi I, K lần lượt là trung điểm HB,HC. Gọi AH cắt DE tại O.CMR:Tam giác OEK vuông, IDEK là hình thang vuông.
c) Gọi M là trung điểm IK, biết BC=10cm.Tính OM?
Bài 1: Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AH. E là giao điểm của BI và AC. Tính các độ dài AE và EC biết AH =12cm; BC = 18cm
Bài 2: Cho tam giác ABC (AC > AB), đường cao AH. Gọi D,E,K theo thứ tự là trung điểm của AB, AC,BC. CMR:
a, DE là đường trung trực của AH
b, DEKH là hình thang cân
Bài 3: Cho tam giác ABC cân tại A, đường cao AH. Gọi D là chân đường vuông góc kẻ từ H đến AC. I là trung điểm của HD.
a, Gọi M là trung điểm của CD. CMR: MI vuông góc với AH
b, CM: AI vuông góc với BD
Cho tam giác ABC vuông tại A có đường cao AH. Gọi D là trung điểm của BC. Kẻ DE vuông góc với AC tại E. Gọi F là điểm đối xứng của E qua D. Gọi M là trung điểm HC. Chứng minh FM vuông góc với AM
Bài 1: Cho tam giác ABC vuông tại A có AB<AC. Gọi M là trung điểm của BC, kẻ MD vuông góc với AB tại D, ME vuông góc với AC tại E. a) Chứng minh AM=DE b) Chứng minh tứ giác DMCE là hình bình hành c) Gọi AH là đường cao của tam giác ABC ( H thuộc BC ). Chứng minh tứ giác DHME là hình thang cân và A đối xứng với H qua DE.
Mình đang cần gấp bài này sáng mai mình kiểm tra. Các bạn giúp mình nhé, cảm ơn các bạn nhiều.
Cho tam giác ABC vuông tại A ( AB < AC ). Gọi M là trung điểm đoạn BC. Vẽ MD vuông góc với AB tại D và ME vuông góc với AC tại E.
a) CM: Tứ giác ADME là hình chữ nhật
b) CM: E là trung điểm của AC. Chứng minh tứ giác CMDE là hình bình hành
c, Vẽ đuờng cao AH của tam giác ABC. CM: Tứ giác MHDE là hình thang cân
d, Qua A vẽ đuờng thẳng // voiứ DH cắt DE tại K. CM: HK vuông góc với AC
Cho tam giác ABC vuông tại A, đường trung tuy n AM, đường cao AH. Gọi D, E theo thứ
tự là chân đường vuông góc kẻ t H n AB, AC. Chứng minh rằng
a) AH = DE b) H ̂ B = M ̂ C
c) AM vuông góc DE
d) Chứng minh DICE là hình thang biết I l trung điểm của HB v K l trung điểm của HC
Cho tam giác ABC vuông tại A (AB < AC) . M là trung điểm cạnh BC. Vẽ MD vuông góc với AB tại D và ME vuông góc với AC tại E.
a) Chứng minh tứ giác ADME là hình chữ nhật.
b) Chứng minh E là trung điểm của đoạn thẳng AC và tứ giác CMDE là hình bình hành.
c) Vẽ đường cao AH của tam giác ABC. Chứng minh tứ giác MHDE là hình thang cân
d) Qua A vẽ đường thẳng song song với DH cắt DE tại K. Chứng minh HK vuông góc với AC.
Cho tam giác ABC vuông tại A (AB<AC). Gọi M là trung điểm của BC, vẽ ME vuông góc AB tại E, MF vuông góc Ac tại F. Gọi D là điểm đối xứng với M qua E. Vẽ đường cao Ah của tam giác ABC.
a) cm AEMF là hcn
b) cm ADBM là hình thoi
c) tính số đo góc EHF
cho ABC vuông tại A (AB<AC).G ọi M là trung điểm BC . Từ M vẽ ME vuông góc vs BA tại E và MN vuông góc vs AC tại N.
a)CM: tứ giác ANME là hình chũ nhật
b)Vẽ đường cao AH của tam giác ABC . CM tứ giác MNEH là hình thang cân