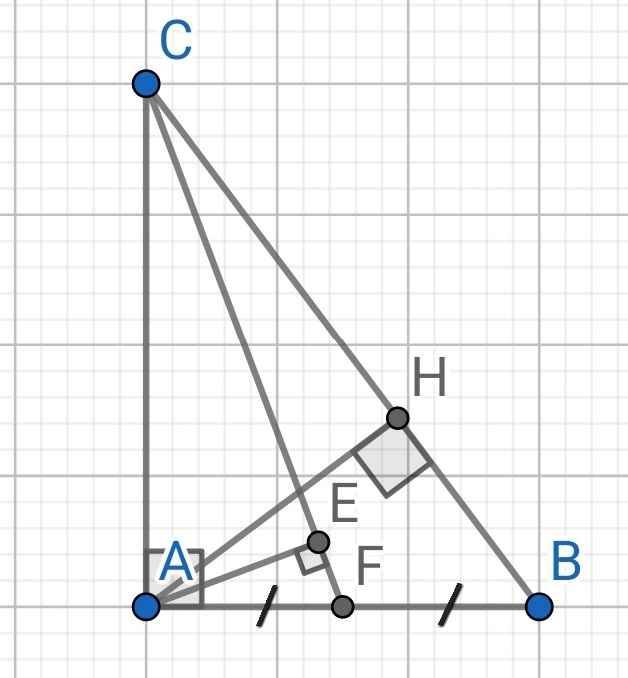
 a) ∆ABC vuông tại A có AH là đường cao
a) ∆ABC vuông tại A có AH là đường cao
⇒ AH² = BH . CH
= 9 . 16
= 144
⇒ AH = 12 (cm)
BC = BH + CH
= 9 + 16
= 25 (cm)
∆ABC vuông tại A có AH là đường cao
⇒ AB² = BH . BC
= 9 . 25
= 225
⇒ AB = 15 (cm)
AC² = CH . BC
= 16 . 25
= 400
⇒ AC = 20 (cm)
b) Do F là trung điểm AB
⇒ AF = AB : 2 = 15 : 2 = 7,5 (cm)
∆ACF vuông tại A
⇒ tanAFC = AC/AF = 20/7,5 = 8,3
⇒ ∠AFC ≈ 69⁰
c) Do AE ⊥ CF (gt)
⇒ AE là đường cao của ∆ACF
∆ACF vuông tại C có CE là đường cao
⇒ AC² = CE.CF (1)
∆ABC vuông tại A có AH là đường cao
⇒ AC² = BC.CH (2)
Từ (1) và (2) suy ra:
CE.CF = BC.CH












