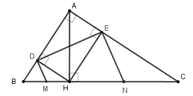
Δ ABC vuông tại A đường cao AH
⇒BH.CH=\(AH^2\)⇒AH=\(\sqrt{9\cdot16}\)=12 cm
BC=CH+BH=9+16=25 cm
\(AB^2\)=BH.BC=9.25=225⇒AB=15 cm
\(AC^2\)=CH.BC=16.25=400⇒AC=20 cm
Ta có:góc A=góc E =góc D=90 nên tứ giác ADHE là hcn
⇒góc AED=góc AHD (1)
lại có:góc AHD=góc ABC (cùng phụ với góc DHB) (2)
Từ (1) và (2) suy ra góc AED = góc ABC
Xét Δ AED và Δ ABC có
góc A chung
góc AED = góc ABC (cmt)
Nên Δ AED = Δ ABC
⇒\(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)⇔AE.AC=AB.AD
c: Xét ΔABH vuông tại H có HD là đường cao ứng với cạnh huyền AB
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔACH vuông tại H có HE là đường cao ứng với cạnh huyền AC
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)