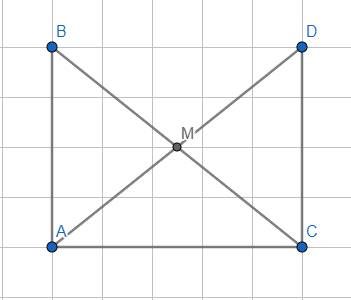
a, Có: AM là trung tuyến ΔABC
\(\Rightarrow\) M là trung điểm BC
\(\Rightarrow MB=MC\)
Xét ΔABM và ΔCDM có:
\(MB=MC\left(cmt\right)\)
\(\widehat{AMB}=\widehat{CMD}\left(đ^2\right)\)
\(MA=MD\)
\(\Rightarrow\) ΔABM = ΔCDM ( c.g.c )
\(\Rightarrow\widehat{BAM}=\widehat{DCM}\left(2gtu\right)\)
\(\Rightarrow AB//CD\)
Mà \(BA⊥AC\)
\(\Rightarrow DC⊥AC\)
b, Có: ΔABM = ΔCDM ( cmt )
\(\Rightarrow\left\{{}\begin{matrix}BA=DC\left(2ctu\right)\\\widehat{ABM}=\widehat{CDM}\left(2gtu\right)\end{matrix}\right.\)
Xét ΔABC và ΔCDA có:
\(\widehat{ABM}=\widehat{CDM}\left(cmt\right)\)
\(AB=CD\left(cmt\right)\)
\(\widehat{BAC}=\widehat{DCA}\left(=90^o\right)\)
\(\Rightarrow\) ΔABC = ΔCDA ( g.c.g )
\(\Rightarrow BC=DA\left(2ctu\right)\)
Có: M là trung điểm BC
M là trung điểm AD ( MA = MD )
Mà \(BC=AD\)
\(\Rightarrow MA=MB\)
\(\Rightarrow\) ΔABM cân tại M
Mà \(\widehat{ABM=60^o}\)
\(\Rightarrow\) ΔABM là tam giác đều.