Xét tam giác ABD và tam giác ACB ta có ;
^BAD = ^BAC = 900
\(\frac{AB}{AC}=\frac{AD}{AB}=\frac{10}{20}=\frac{5}{10}=\frac{1}{2}\)
Vậy tam giác ABD ~ tam giác ACB ( c.g.c )
=> ^ABD = ^ACB ( 2 góc tương ứng )
Xét tam giác ABD và tam giác ACB ta có ;
^BAD = ^BAC = 900
\(\frac{AB}{AC}=\frac{AD}{AB}=\frac{10}{20}=\frac{5}{10}=\frac{1}{2}\)
Vậy tam giác ABD ~ tam giác ACB ( c.g.c )
=> ^ABD = ^ACB ( 2 góc tương ứng )
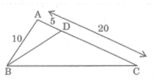
Cho tam giác ABC có AB = 10cm, AC=20cm. Trên cạnh AC, đặt đoạn AD = 5cm. Chứng minh: ∠ (ABD) = ∠ (ACB)
B1:Cho tam giác ABC có AB=12cm, AC=15cm, BC=18cm. Trên cạnh AB, đặt đoạn thẳng AM=10cm trên AC đặt đoạn thẳng AN=8cm. Tính độ dài đoạn thẳng MN
B2:Cho tam giác ABC có AB=10, AC=20cm. Trên cạnh AB, đặt đoạn thẳng AD=5cm. Chứng minh góc ABD=gốc ACB
Câu 1: Cho tam giác ABC có AB < AC. Trên cạnh AC lấy điểm D sao cho góc ABD = góc ACB
a) Chứng minh: Tam giác ABD đồng dạng với tam giác ACB và viết tỉ số đồng dạng
b) Chứng minh: AB2 = AD . AC
- Giúp mình với nhé, mình cảm ơn nhiều
Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm. Vẽ đường cao AD của tam giác ABC. a) Chứng minh tam giác ABC vuông tại A và tam giác ABD đồng dạng tam giác CAD. b) Trên AB lấy điểm F sao cho AB = 3AF. Từ điểm D, vẽ đường thẳng vuông góc với FD tại D, đường thẳng này cắt AC tại E. Chứng minh: góc AFD = góc CED. c) Tính tỉ số:
Cho tam giác ABC vuông tại A có AB=15cm, AC=20cm, kẻ đường cao AH. Phân giác của góc HAC cắt BC tại D.
a) Chứng minh tam giác ABD cân
b) Trên cạnh AC lấy điểm E sao cho AE=AH. Chứng minh CE.CA=CD.CH
c) Chứng minh DC/DH=AC/AE.
Cho tam giác ABC vuông tại A, Đường cao AH, AB<AC. Trên AC lấy D sao cho AD=AB. Gọi I là trung điểm của BD. Chứng minh góc BIH bằng góc ACB
Cho tam giác ABC có ba cạnh AB = 14cm, AC = 20cm và BC = 18cm. Trên cạnh AB lấy điểm E sao cho AE = 10cm. Trên cạnh AC lấy điểm D sao cho AD = 7cm.
a/ Chứng minh tam giác ADE ~ tam giác ABC
b/ Tính DE
Bài 1:
Cho góc xAy khác góc bẹt, trên cạnh Ax lấy điểm B sao cho AB=5cm, trên cạnh Ay lần lượt lấy hai điểm C và D sao cho AC = 4cm, AD = 10. Qua D kẻ đường thẳng song song với BC cắt Ax tại E. Tính BE và tỉ số diện tích. hai tam giác ABC và AED.
Bài 2:
a) Cho tam giác ABC có AB = 6cm, AC = 9cm, BC =10cm, đường, phân giác AD, D thuộc BC. Tính DB, DC.
b) Trên cạnh AC lấy điểm E sao cho góc AEB = góc ADB. Gọi M là giao điểm của BE và AD. Chứng minh hai tam giác AME và tam giác BMD đồng dạng.
Bài 3:
Cột cờ của trường vào những ngày có năng, lúc 14 giờ thường có bóng dài 10m, cùng lúc đó một học sinh đứng ở sân trường thì có bóng dỗ dài 1m, biết rằng em học sinh đó cao 1,5m. Hỏi cột cờ của trường cao bao nhiêu mét?
Bài 4:
Cho tam giác ABC vuông tại A, M là điểm di chuyển trên cạnh AC, M khác A và C. Vẽ đường thẳng Cx vuông góc với tia BM tại H, CA cắt tia BA tại D.
a) Chứng minh hai tam giác DHB và tam giác DAC đồng dạng.
b) Chứng tỏ góc AHD có số đo không đổi khi M di chuyển trên cạnh AC
cho tam giác abc có ab=15, ac=21cm, bc=30cm.trên ab lấy điểm e sao cho ae=7cm trên cạnh ac lấy d sao cho ad= 5cm. a) chứng minh tam giác abd đồng dạng tam giác ace.b) tính tỉ số diện tích của tam giác abd và tam giác ace