Các câu hỏi tương tự
Cho nửa đường tròn (O;R), đường kính BC và điểm A thuộc nửa đường tròn đó. Dựng về phía ngoài tam giác ABC hai nửa đường tròn: nửa đường tròn tâm I, đường kính AB; nửa đường tròn tâm K đường kính AC. Một đường thẳng d thay đổi qua A cắt nửa đường tròn (I) và (K) tương ứng tại M và N.a) Tứ giác MNCB là hình gì ?b) CM: AM.AN MB.NCc) CM: tam giác OMN là tam giác când) Xác định vị trí của đường thẳng d để diện tích tứ giác BMNC lớn nhất.
Đọc tiếp
Cho nửa đường tròn (O;R), đường kính BC và điểm A thuộc nửa đường tròn đó. Dựng về phía ngoài tam giác ABC hai nửa đường tròn: nửa đường tròn tâm I, đường kính AB; nửa đường tròn tâm K đường kính AC. Một đường thẳng d thay đổi qua A cắt nửa đường tròn (I) và (K) tương ứng tại M và N.
a) Tứ giác MNCB là hình gì ?
b) CM: AM.AN = MB.NC
c) CM: tam giác OMN là tam giác cân
d) Xác định vị trí của đường thẳng d để diện tích tứ giác BMNC lớn nhất.
Cho nửa đường tròn (O;R), đường kính BC và điểm A thuộc nửa đường tròn đó. Dựng về phía ngoài tam giác ABC hai nửa đường tròn: nửa đường tròn tâm I, đường kính AB; nửa đường tròn tâm K đường kính AC. Một đường thẳng d thay đổi qua A cắt nửa đường tròn (I) và (K) tương ứng tại M và N.a) Tứ giác MNCB là hình gì ?b) CM: AM.AN MB.NCc) CM: tam giác OMN là tam giác când) Xác định vị trí của đường thẳng d để diện tích tứ giác BMNC lớn nhất.
Đọc tiếp
Cho nửa đường tròn (O;R), đường kính BC và điểm A thuộc nửa đường tròn đó. Dựng về phía ngoài tam giác ABC hai nửa đường tròn: nửa đường tròn tâm I, đường kính AB; nửa đường tròn tâm K đường kính AC. Một đường thẳng d thay đổi qua A cắt nửa đường tròn (I) và (K) tương ứng tại M và N.
a) Tứ giác MNCB là hình gì ?
b) CM: AM.AN = MB.NC
c) CM: tam giác OMN là tam giác cân
d) Xác định vị trí của đường thẳng d để diện tích tứ giác BMNC lớn nhất.
cho đường tròn tâm O, đường kính AB và một điểm C di động trên AB. Vẽ các đường tròn tâm I đường kính AC và đường tròn tâm K đường kính BC. Tia Cx vuông góc với AB tại C, cắt (O) tại M. Đoạn thẳng MA cắt đường tròn (I) tại E và đoạn thẳng MB cắt đường tròn (K) tại F.a) chứng minh tứ giác MECF là hcn và EF là tiếp tuyến chung của (I) và (K)b) cho AB4cm, xác định điểm C trên AB để diện tích tứ giác IEKF là lớn nhấtc) khi C khác O đường tròn ngoại tiếp hcn MECF cắt đường tròn (O) tại P ( khác M), đ...
Đọc tiếp
cho đường tròn tâm O, đường kính AB và một điểm C di động trên AB. Vẽ các đường tròn tâm I đường kính AC và đường tròn tâm K đường kính BC. Tia Cx vuông góc với AB tại C, cắt (O) tại M. Đoạn thẳng MA cắt đường tròn (I) tại E và đoạn thẳng MB cắt đường tròn (K) tại F.
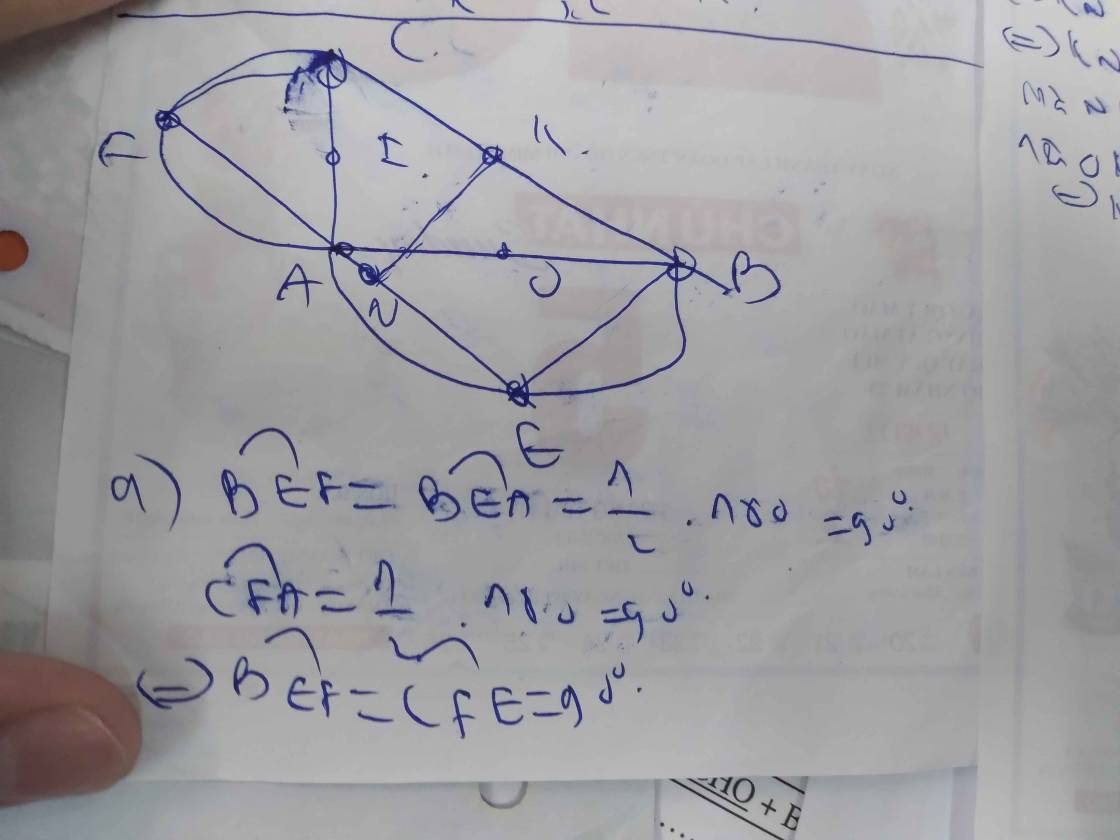
a) chứng minh tứ giác MECF là hcn và EF là tiếp tuyến chung của (I) và (K)
b) cho AB=4cm, xác định điểm C trên AB để diện tích tứ giác IEKF là lớn nhất
c) khi C khác O đường tròn ngoại tiếp hcn MECF cắt đường tròn (O) tại P ( khác M), đường thẳng PM cắt AB tại N. Chứng minh tam giác MPF đồng dạng với tam giác MBN.
d) chứng minh 3 điểm N,E,F thẳng hàng.
1 . Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn tâm I, đường kính AH cắt AB, AC lần lượt tại M và N, D là giao điểm của MN và OAa) chứng minh AM.ABAN.AC và tứ giác BMNC nội tiếpb) cm tam giác ADI đồng dạng tam giác AHOc) gọi E là giao điểm BC và NM, K là giao điểm AE và (I). cm góc BKC 90°2 . Cho tam giác ABC nhọn, BC AC, đường tròn tâm O đường kính BC cắt AB,AC tại E,F. BF cắt CE tại H, AH cắt BC tại D.a) Chứng minh: AD vuông góc BCb) Chứng minh: AD là đường phân giác của góc ED...
Đọc tiếp
1 .
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn tâm I, đường kính AH cắt AB, AC lần lượt tại M và N, D là giao điểm của MN và OA
a) chứng minh AM.AB=AN.AC và tứ giác BMNC nội tiếp
b) cm tam giác ADI đồng dạng tam giác AHO
c) gọi E là giao điểm BC và NM, K là giao điểm AE và (I). cm góc BKC = 90°
2 .
Cho tam giác ABC nhọn, BC = AC, đường tròn tâm O đường kính BC cắt AB,AC tại E,F. BF cắt CE tại H, AH cắt BC tại D.
a) Chứng minh: AD vuông góc BC
b) Chứng minh: AD là đường phân giác của góc EDF
c) Đường tròn đường kính EC cắt AC tại M, BM cắt (O) tại K. Chứng minh: KC đi qua trung điểm của HF
từ điểm A ở ngoài đường tròn tâm o , kẻ 2 tiếp tuyến ABvà AC với dường tròn (B,C là các tiếp điểm )
a)cm tam giác abc cân và ao vuông với bc
b) vẽ đường kính COD, đường thẳng qua o và vuông góc CD cắt BD tại E .
cm tứ giác OAEB là hình thang cân
cho đường tròn (O;R) và điểm A nằm ngoài đường tròn. từ A vẽ 2 tiếp tuyến AB,AC (B; c là các tiếp điểm). gọi H là giao điểm OA và BC
a) Qua O vẽ đường vuông góc với OB cắt AC tại M. cm tam giác AMO cân
b) qua A vẽ đường thẳng không đi qua tâm cắt đường tròn (O) tại E và F (E nằm giữa A và F), K là trung điểm EF, tia OK cắt BC tại S. cm: SE là tiếp tuyến của (O)
mk cần gấpCho tam giác ABC nội tiếp đường tròn tâm O đường kính AB sao cho ACAB. E là một điểm thuộc BC(E# B,C).Tia AE cắt đường tròn tại điểm thứ 2 là D, kẻ EH vuông góc với AB tại Ha. Cm ACEH nội tiếpb.Tia CH cắt (O) tại điểm thứ hai là F. Cm EH//DFc.CMR đường tròn ngoại tiếp tam giác CHO đi qua Dd. Gọi I và K lần lượt là hình chiếc vuông góc của F trên các đường thẳng CA và CB. CMR:AB,DF,IK đi qua 1 điểm
Đọc tiếp
mk cần gấp
Cho tam giác ABC nội tiếp đường tròn tâm O đường kính AB sao cho AC<AB. E là một điểm thuộc BC(E# B,C).Tia AE cắt đường tròn tại điểm thứ 2 là D, kẻ EH vuông góc với AB tại H
a. Cm ACEH nội tiếp
b.Tia CH cắt (O) tại điểm thứ hai là F. Cm EH//DF
c.CMR đường tròn ngoại tiếp tam giác CHO đi qua D
d. Gọi I và K lần lượt là hình chiếc vuông góc của F trên các đường thẳng CA và CB. CMR:AB,DF,IK đi qua 1 điểm
Cho tam giác nhọn ABC đường tròn tâm ( O) , đường kính BC cắt AB , AC lần lượt tại D và E . Hai đường thẳng BD, CE cắt nhau tại H. Gọi F là giao điểm của AH và BC
a/ cm: AD.ABAE.AC
b/ cm: (DEF) đi qua O của BC và trung điểm I của AH
c/ nếu BC=12 và A^ bằng 60°. Tính OI
Xem chi tiết
1/ Từ một điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MB( A,B là tiếp điểm) a/ CMR tứ giác MAOB nội tiếp định tâm I và bán kính của đường tròn nàyb/ Cho MO 2R CMR tam giác MAB đều 2/ Cho đường tròn (O) đường kính AB gọi I là trung điểm của OA. Qua I vẽ dây CD vuông góc AB. K la trung điểm của BC. CMR tứ giác CIOK nội tiếp đường tròn3/ Cho nửa đường tròn (O) đường kính AB. Từ A và B kẻ hai tiếp tuyến Ax, By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt Ax và By lần lượt tại...
Đọc tiếp
1/ Từ một điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MB( A,B là tiếp điểm)
a/ CMR tứ giác MAOB nội tiếp định tâm I và bán kính của đường tròn này
b/ Cho MO = 2R CMR tam giác MAB đều
2/ Cho đường tròn (O) đường kính AB gọi I là trung điểm của OA. Qua I vẽ dây CD vuông góc AB. K la trung điểm của BC. CMR tứ giác CIOK nội tiếp đường tròn
3/ Cho nửa đường tròn (O) đường kính AB. Từ A và B kẻ hai tiếp tuyến Ax, By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt Ax và By lần lượt tại E và F. CMR tứ giác AEMO là tứ giác nội tiếp
4/ Cho tam giác ABC cân tại A có góc A nhọn, đường vuông góc với AB tại A cắt đường thẳng B, C tại E. Kẻ EN vuông với EC gọi M là trung điểm BC. CMR tứ giác AMNE là tứ giác nội tiếp đường tròn
Giải giúp mk vs mk đang cần gấp