Các câu hỏi tương tự
Cho hình chóp S.ABC có ABC là tam giác vuông tại B, AB a, BC 2a. Biết
S
A
⊥
A
B
,
S
C
⊥
B
C
, góc giữa SC và (ABC) bằng
60
0
. Độ dài cạnh SB bằng: A.
2
a
B.
2
2
a...
Đọc tiếp
Cho hình chóp S.ABC có ABC là tam giác vuông tại B, AB = a, BC = 2a. Biết S A ⊥ A B , S C ⊥ B C , góc giữa SC và (ABC) bằng 60 0 . Độ dài cạnh SB bằng:
A. 2 a
B. 2 2 a
C. 3 a
D. 3 2 a
Cho hình lăng trụ ABC.A’B’C’ độ dài cạnh bên là 2a, dáy ABC là tam giác vuông tại A, AB a, AC
a
3
. Hình chiếu của A’ lên (ABC) trùng với trung điểm I của BC. Khi đó cos(AA;BC) là:
A
.
1
2
B
.
1
4
C
.
2
2
D
....
Đọc tiếp
Cho hình lăng trụ ABC.A’B’C’ độ dài cạnh bên là 2a, dáy ABC là tam giác vuông tại A, AB = a, AC = a 3 . Hình chiếu của A’ lên (ABC) trùng với trung điểm I của BC. Khi đó cos(AA';B'C') là:
A . 1 2
B . 1 4
C . 2 2
D . 3 2
Trong không gian cho tam giác ABC vuông tại A có AB a, AC
a
3
. Tính độ dài đường sinh l của hình nón nhận được khi quay tam giác ABC xung quanh trục AB. A. l
a
3
B. l
a
2
C. l
(
1
+
3
)
a
D. l 2a
Đọc tiếp
Trong không gian cho tam giác ABC vuông tại A có AB = a, AC = a 3 . Tính độ dài đường sinh l của hình nón nhận được khi quay tam giác ABC xung quanh trục AB.
A. l = a 3
B. l= a 2
C. l = ( 1 + 3 ) a
D. l = 2a
Tứ diện SABC có ba đỉnh A, B, C tạo thành tam giác vuông cân đỉnh B và AC 2a, có cạnh SA vuông góc với mặt phẳng (ABC) và SA aa) Chứng minh mặt phẳng (SAB) vuông góc với mặt phẳng (SBC).b) Trong mặt phẳng (SAB) vẽ AH vuông góc với SB tại H, chứng minh AH ⊥ (SBC).C) Tính độ dài đoạn AH.d) Từ trung điểm O của đoạn AC vẽ OK vuông góc với (SBC) cắt (SBC) tại K. Tính độ dài đoạn OK.
Đọc tiếp
Tứ diện SABC có ba đỉnh A, B, C tạo thành tam giác vuông cân đỉnh B và AC = 2a, có cạnh SA vuông góc với mặt phẳng (ABC) và SA = a
a) Chứng minh mặt phẳng (SAB) vuông góc với mặt phẳng (SBC).
b) Trong mặt phẳng (SAB) vẽ AH vuông góc với SB tại H, chứng minh AH ⊥ (SBC).
C) Tính độ dài đoạn AH.
d) Từ trung điểm O của đoạn AC vẽ OK vuông góc với (SBC) cắt (SBC) tại K. Tính độ dài đoạn OK.
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B và có độ dài các cạnh AB = BC = 6, AD=12. Tam giác SAC vuông tại S. và có hình chiếu của S xuống (ABCD) là H thỏa mãn AC=34H. Gọi M, N lần lượt là trung điểm của SB,CD . Tinh tan (MN,(SAC))
Cho tam giác ABC cân tại A. Biết rằng độ dài cạnh BC, trung tuyến AM và độ dài cạnh AB theo thứ tự đó lập thành một cấp số nhân có công bội q. Tìm công bội q của cấp số nhân đó A.
q
1
+
2
2
B.
q...
Đọc tiếp
Cho tam giác ABC cân tại A. Biết rằng độ dài cạnh BC, trung tuyến AM và độ dài cạnh AB theo thứ tự đó lập thành một cấp số nhân có công bội q. Tìm công bội q của cấp số nhân đó
A. q = 1 + 2 2
B. q = 2 + 2 2 2
C. q = - 1 + 2 2
D. q = - 2 + 2 2 2
hình chóp SABC có đáy ABC là tam giác vuông cân tại C tam giác SAB vuông cân tại S và SBC = 60 độ gọi M là trung điểm của cạnh SB, Cos góc giữa đường thẳng AB và CM là?
Xem chi tiết
Cho tam giác ABC vuông cân đỉnh C, AB
2
. Tính độ dài của
A
B
→
+
A
C
→
A. B. C. D.
Đọc tiếp
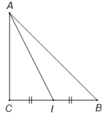
Cho tam giác ABC vuông cân đỉnh C, AB = 2 . Tính độ dài của A B → + A C →
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho tam giác ABC vuông tại A, cạnh AB 6, AC 8 và M là trung điểm của cạnh AC. Khi đó thể tích của khối tròn xoay do tam giác BMC quanh một vòng quanh cạnh AB là
Đọc tiếp
Cho tam giác ABC vuông tại A, cạnh AB = 6, AC = 8 và M là trung điểm của cạnh AC. Khi đó thể tích của khối tròn xoay do tam giác BMC quanh một vòng quanh cạnh AB là
![]()
![]()
![]()
![]()




