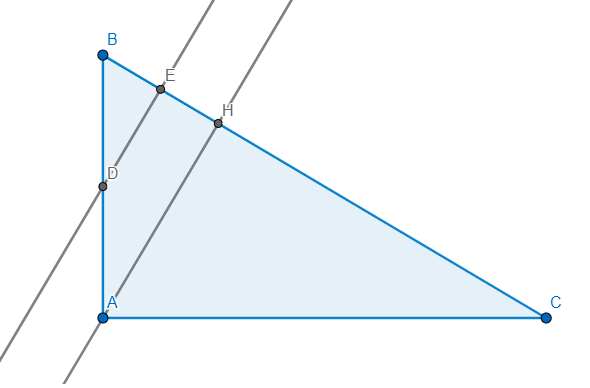
Vẽ đường cao AH \(\Rightarrow DE\parallel AH(\bot BC)\) mà D là trung điểm AB
\(\Rightarrow E\) là trung điểm BH \(\Rightarrow EB=EH\)
Ta có: \(EC^2-EB^2=\left(EC-EB\right)\left(EC+EB\right)=\left(EC-BH\right)BC\)
\(=CH.BC\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AC^2=CH.BC\Rightarrow AC^2=EC^2-EB^2\)
cho tam giác ABC vuông ở A từ trung điểm D của AB vẽ DE vuông góc với BC CM \(EC^2-EB^2=AC^2\)
Cho tam giác ABC vuông tại A , từ trung điểm D của AB vẽ DE vuông góc với BC . Chứng minh : EC-EB=AC2
Cho tam giác ABC vuông tại A từ trung điểm D của AB vẽ DE vuông góc với BC chứng minh rằng EC^2 - EB^2=AC^2
Cho tam giác ABC cân tại A, có góc A nhọn. Từ A vẽ đường thẳng vuông góc AB, đường thẳng này cắt BC tại D. Đường tròn tâm K đường kính AD cắt DC và AC lần lượt tại H và E. a) CM: Tam giác AHD và tam giác AED vuông. b) CM: H là trung điểm BC c) AH^2 =HC.HD d) CM DH là tia phân giác của góc ADE. CM KH song song DE
Cho tam giác ABC vuông tại A có AB=36 cm, AC =48 cm.M là trung điểm của BC. Đường vuông góc với BC tại M cắt các đường thẳng AC, BC ở D, E.
a) CMR: Tam giác ABC đồng dạng với tam giác MDC
b) Tính các cạnh của tam giác MDC
c) Tính BE, EC
Cho tam giác ABC vuông tại A (AB<AC) , AH vuông góc với BC
a. Từ B kẻ đường thẳng vuông góc với trung tuyến AM cắt AH tại D , AM tại E , AC tại F.
CM : D là trung điểm của BF
BE.BF =BH.BC
b , Cho AB =120 cm ; AC =160 cm . Tính DE; AF .
Bài 1.Cho tam giác ABC có trọng tâm G. Đường thẳng d đi qua G cắt hai cạnh AB và AC. CMR khoảng cách từ A đến d bằng tổng các khoảng cách từ B và C đến d.
Bài 2. Cho tam giác ABC cân tại A và đường cao AD. Từ D dựng DE vuông góc AB và DF vuông góc AC (E thuộc AB, F thuộc AC)
a) Chứng minh AD là trung trực của đoạn EF.
[B]b) [/B]Trên tia đối của tia DE lấy điểm G sao cho DG=DE. Chứng minh tam giác CEG vuông.
Bài 3. Cho tam giác ABC, vẽ tam giác vuông cân ABD cân tại B,A và D ở hai nửa mặt phẳng đối nhau bờ là đường thẳng BC. Vẽ tam giác vuông cân CBG cân tại B,G và A ở cùng nửa mặt phẳng bờ là đường thẳng BC. Chứng minh rằng GA vuông góc vớ DC.
Bài 4.Cho tam giác ABC trên tia đối của tia BA, CA lần lượt lấy điểm P,Q sao cho BP=CQ. Gọi M,N lần lượt là trung điểm của các đoạn BC,PQ. Đường thẳng MN cắt đường thẩngB,AC theo thứ tự tại B' và C'. Chứng minh rằng tam giác B'AC cân.
cho tam giác có 2 góc B và C nhọn ,AB=16cm, AC=12cm .Từ trung điểm D của AC vẽ DI vuông góc BC tại I viết CI =3,6cm
CM tam giác ABC vuông tại A
Cho tam giac ABC có AB = 12 cm, AC = 16 cm, BC = 20 cm, đường cao AH
a) Chứng minh tam giác ABC là tam giác vuông
b) Tính AH, BH và tỉ số lượng giác của góc B
c) Từ một điểm D trên cạnh AB kẻ đường thẳng song song với BC cắt cạnh AC tạ E tìm D sao cho BD + EC = DE
