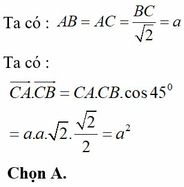Các câu hỏi tương tự
Cho tam giác ABC vuông cân tại A, M là trung điểm BC. Lấy điểm D bất kì thuộc cạnh BC. H và I thứ tự là hình chiếu của B và C xuống đường thẳng AD. Đường thẳng AM cắt CI tại N. Chứng minh rằng:
a) BH = AI.
b) BH^2 + CI^2 = 2AM^2
c) IM là phân giác của góc HIC
Cho tam giác ABC cân tại A .trên tia đối của tia BA vàCA lấy 2 điểm D,E sao cho BD=CE.
a/ chứng minh DE//BC
b/ Từ D kẻ DM vuông gó với BC,EN vuông góc với BC. cHỨNG MINH BM=CN
c/ Chứng minh tam giac AMN cân
d/Từ B và C kẻ các đường vuông góc với AM, AN chúng cắt nhau tại I . Chứng minh rằng AI là tia phân giác chung của hai góc BAC và MAN.
a) cho tam giác ABC . Chứng minh rằng : sin( B + C ) = sinA và cos \(\frac{A+B}{2}\) = sinC ; b) cho tam giác ABC có vector BA nhân vector BC = AB2 . Chứng minh rằng : tam giác ABC vuông ; c) chứng minh rằng : sin6a + cos6a + 3sin2acos2a = 1
Cho tam giác ABC cân tại A có 2 đường phân giâc BD bà CE cắt nhau tại i
a) BEDC là hình gì, vì sao ?
b) chứng minh : BE = ED = DC
c) chứng minh AI là đường trung trực của DE và BC
d) góc A = 50 tính các góc của tứ giác BEDC
1.Trên mp có 11 đường thẳng đôi 1 ko song song C/m:có 2 đường thẳng tạo với nhau 1 góc 17 độ2.Cho (O) đường kính AB.Lấy C ngoài đoạn thẳng AB (C nằm trên đường thẳng AB).Kẻ 2 tiếp tuyến CE và CF. AB cắt EF tại I, kẻ cát tuyến CMN. C/m: góc AIM góc BIN3.Cho tam giác ABC ngoại tiếp đường tròn (O).Biết D,E,F là các tiếp điểm , D thuộc AC, E thuộc AB, F thuộc BC Biết OEr, ABc, ACb, BCaC/m:a) (a+b+c)*r2S ( S là diện tích tam giác ABC)b)nếu (a+b+c)(a+b-c)4S thì tam giác ABC vuông
Đọc tiếp
1.Trên mp có 11 đường thẳng đôi 1 ko song song C/m:có 2 đường thẳng tạo với nhau 1 góc <17 độ
2.Cho (O) đường kính AB.Lấy C ngoài đoạn thẳng AB (C nằm trên đường thẳng AB).Kẻ 2 tiếp tuyến CE và CF. AB cắt EF tại I, kẻ cát tuyến CMN. C/m: góc AIM= góc BIN
3.Cho tam giác ABC ngoại tiếp đường tròn (O).Biết D,E,F là các tiếp điểm , D thuộc AC, E thuộc AB, F thuộc BC Biết OE=r, AB=c, AC=b, BC=a
C/m:a) (a+b+c)*r=2S ( S là diện tích tam giác ABC)
b)nếu (a+b+c)(a+b-c)=4S thì tam giác ABC vuông
Cho tam giác ABC vuông cân tại A, M là trung điểm BC. Lấy điểm D bất kì thuộc cạnh BC. H và I thứ tự là hình chiếu của B và C xuống đường thẳng AD. Ta có tỉ số BC2 / BH2 + CI2 không đổi và có giá trị bằng
Cho tam giác ABC vuông cân tại A , M là trung điểm cạnh BC. Điểm E nằm giữa M và C, vẽ BH vuông góc với AE tại K. Chứng minh:
a/ BH = AK
b/ tam giác HBM = tam giác KAM
c/ Tam giác MHK vuông cân
Cho tam giác ABC vuông tại A (AB<AC) có AB = 6cm, BC = 10cm
a) Tính độ dài AC
b) Trên tia đối của tia AB lấy điểm D sao cho AD = AB
Chứng minh: tam giác ABC = tam giác ADC
c) Qua A vẽ đường thẳng song song với BC cắt DC tại E
Chứng minh: Tam giác AEC cân tại E
d) Gọi F là trung điểm của BC. Trên AC lấy điểm O sao cho AC = 3AO
Chứng minh ba điểm F, O, D thẳng hàng.
Cho tam giác ABC vuông tại A có AB= 9cm ; BC=10cm
a. Tính AC và so sánh các góc tam giác ABC
b. Trên tia đối tia AB lấy điểm D sao cho A là trung điểm BD. Chứng minh tam giác BCD cân
c. Gọi E; F lần lượt là trung điểm các cạnh DC, BC. Đường thẳng BE cắt cạnh AC tại M.
Tính CM và chứng minh 3 điểm D; M; F thẳng hàng
cho tam giác abc vuông tại a có ab=6cm,ac=8cm. Vẽ đường cao ah.
a)tính bc,ah
b)cm:tam giác hab đồng dạng tam giác hac =>bh.ch=\(ah^2\)
c)trên bc lấy điểm e sao cho ce=4cm.cm:\(be^2=bh.ch\)
d)tia phân giác của góc abc cắt ac tại d.tính\(\Delta_{CED}\)
GIẢI GIÙM MÌNH NHANH NHANH NHE