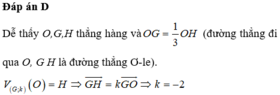Các câu hỏi tương tự
Cho mặt phẳng Oxy cho tam giác ABC có A(-1; 2), B(-2; -4), C(1; 2)1) Viết phương trình tổng quát đường thẳng AC, phương trình tham số đường trung tuyến CM.2) Tìm tọa độ trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp I của tam giác ABC.3) Tính chu vi, diện tích tam giác ABC.4) Tính số đo góc tạo bởi 2 đường thẳng AB và AC. 5) Viết phương trình đường tròn ngoại tiếp tam giác ABC. Lập phương trình tiếp tuyến của đường tròn tại điểm A.6) Lập phương trình đường tròn tâm C và tiếp xúc với đường th...
Đọc tiếp
Cho mặt phẳng Oxy cho tam giác ABC có A(-1; 2), B(-2; -4), C(1; 2)
1) Viết phương trình tổng quát đường thẳng AC, phương trình tham số đường trung tuyến CM.
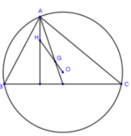
2) Tìm tọa độ trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp I của tam giác ABC.
3) Tính chu vi, diện tích tam giác ABC.
4) Tính số đo góc tạo bởi 2 đường thẳng AB và AC.
5) Viết phương trình đường tròn ngoại tiếp tam giác ABC. Lập phương trình tiếp tuyến của đường tròn tại điểm A.
6) Lập phương trình đường tròn tâm C và tiếp xúc với đường thẳng AB.
Phép vị tự tâm O(0;0) tỉ số k 3 biến đường tròn
(
C
)
:
(
x
-
1
)
2
+
(
y
+
1
)
2
1
thành đường tròn có phương trình: A.
(
x
-
1
)
2
+...
Đọc tiếp
Phép vị tự tâm O(0;0) tỉ số k = 3 biến đường tròn ( C ) : ( x - 1 ) 2 + ( y + 1 ) 2 = 1 thành đường tròn có phương trình:
A. ( x - 1 ) 2 + ( y + 1 ) 2 = 9
B. ( x + 3 ) 2 + ( y - 3 ) 2 = 1
C. ( x - 3 ) 2 + ( y + 3 ) 2 = 9
D. ( x + 3 ) 2 + ( y - 3 ) 2 = 9
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình
(
x
-
1
)
2
+
(
y
-
2
)
2
. Hỏi phép vị tự tâm O tỉ số k -2 biến (C) thành đường tròn nào sau đây: A.
(
x
-
4
)
2...
Đọc tiếp
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình ( x - 1 ) 2 + ( y - 2 ) 2 . Hỏi phép vị tự tâm O tỉ số k = -2 biến (C) thành đường tròn nào sau đây:
A. ( x - 4 ) 2 + ( y - 2 ) 2 = 16
B. ( x - 2 ) 2 + ( y - 4 ) 2 = 16
C. ( x + 2 ) 2 + ( y + 4 ) 2 = 16
D. ( x - 4 ) 2 + ( y - 2 ) 2 = 4
Cho tam giác ABC có A(1;2),B(5;4),C(3;-2). Gọi A',B',C' lần lượt là ảnh của A, B, C qua phép vị tự tâm I(1;5), tỉ số k = -3. Bán kính đường tròn ngoại tiếp tam giác A'B'C' bằng
A. 3 10
B. 6 10
C. 2 5
D. 3 5
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình
x
−
1
2
+
y
−
2
2
4
, phép vị tự tâm O tỉ số k-2 biến k -2 thành đường tròng có phương trình? A.
x
+
1...
Đọc tiếp
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x − 1 2 + y − 2 2 = 4 , phép vị tự tâm O tỉ số k=-2 biến k= -2 thành đường tròng có phương trình?
A. x + 1 2 + y − 2 2 = 16
B. x − 2 2 + y − 40 2 = 4
C. x + 2 2 + y + 4 2 = 16
D. x − 1 2 + y + 2 2 = 4
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình
x
−
1
2
+
y
−
1
2
4.
Phép vị tự tâm O (với O là gốc tọa độ) tỉ số
k
2
biến (C) thành đường tròn nào trong các đường tròn có phương trình sau? A. ...
Đọc tiếp
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x − 1 2 + y − 1 2 = 4. Phép vị tự tâm O (với O là gốc tọa độ) tỉ số k = 2 biến (C) thành đường tròn nào trong các đường tròn có phương trình sau?
A. x − 1 2 + y − 1 2 = 8.
B. x − 2 2 + y − 2 2 = 8.
C. x + 2 2 + y + 2 2 = 16.
D. x − 2 2 + y − 2 2 = 16.
Với phép vị tự tâm O tỉ số k -1 biến đường tròn (C):
x
2
+
y
2
9
thành đường tròn có phương trình nào sau đây? A.
(
x
+
1
)
2
+
(
y
+
1
)
2
9
B.
(
x
-...
Đọc tiếp
Với phép vị tự tâm O tỉ số k= -1 biến đường tròn (C): x 2 + y 2 = 9 thành đường tròn có phương trình nào sau đây?
A. ( x + 1 ) 2 + ( y + 1 ) 2 = 9
B. ( x - 1 ) 2 + ( y - 1 ) 2 = 9
C. ( x - 1 ) 2 + ( y + 1 ) 2 = 9
D. x 2 + y 2 = 9
Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k 2 và phép đối xứng tâm I biến tứ giác IGHF thành A. AIFD B. BCFI C. CIEB D. DIEA
Đọc tiếp
Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm I biến tứ giác IGHF thành
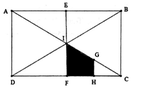
A. AIFD
B. BCFI
C. CIEB
D. DIEA
cho tam giác ABC biết A(3 -7) trực tâm H(3 -1) tâm đường tròn ngoại tiếp là I(-2;0). tìm tọa độ C biết C có hoành độ dương