Các câu hỏi tương tự
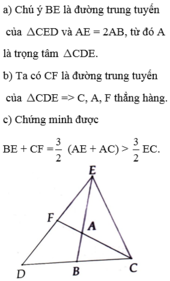
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm E sao cho AE = 2AB. Trên tia đối của tia BC lấy điểm D sao cho BD = BC. Chứng minh:
a) A là trọng tâm của tam giác CDE;
b) Đường thẳng CA đi qua trung điểm của DE.
Cho tam giác ABC, gọi M là trung điểm cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh AB = CD và AB //CD.
b) Chứng minh BD// AC.
c) Chứng minh ∆ A B C = ∆ D C B .
d) Trên các đoạn thẳng AB,CD lần lượt lấy các điểm E, F sao cho AE = DF. Chứng minh, ba điểm E, M, F thẳng hàng.
Cho tam giác ABC, trung tuyên AM. Trên tia đối của tia MA lấy D sao cho MD MA.a) Chứng minh AB // CD và AB CD.b) Gọi E và F lần lượt là trung điểm của AC và BD. AF cắt BC tại I, DE cắt BC tại K. Chứng minh I là trọng tâm tam giác ABD, K là trọng tâm tam giác ACD.c) Chứng minh BI IK KC.d) Chứng minh E, M, F thẳng hàng.
Đọc tiếp
Cho tam giác ABC, trung tuyên AM. Trên tia đối của tia MA lấy D sao cho MD = MA.
a) Chứng minh AB // CD và AB = CD.
b) Gọi E và F lần lượt là trung điểm của AC và BD. AF cắt BC tại I, DE cắt BC tại K. Chứng minh I là trọng tâm tam giác ABD, K là trọng tâm tam giác ACD.
c) Chứng minh BI = IK = KC.
d) Chứng minh E, M, F thẳng hàng.
Cho tam giác ABC có AB < AC. Trên cạnh AC lấy AD = AB. Gọi E là trung điểm của BD. A) chứng minh AE là tia phân giác của góc BAC. B) Chứng minh AE vuông góc với BD. C) Tia AE cắt cạnh BC tại F. chứng minh BF = FD. D) Trên tia đối của tia BA lấy G sao cho BG = CD. Chứng minh G, F, D thẳng hàng.
Cho tam giác ABC, trung tuyến AM và trọng tâm G. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE CF.a) Chứng minh G là trọng tâm tam giác AEF.b) Gọi N là trung điểm của AF. Chứng minh ba điểm E, G, N thẳng hàng.c) Gọi H là trung điểm của GA, I là trung điểm GE. Chứng minh IH // MN và IH MN.
Đọc tiếp
Cho tam giác ABC, trung tuyến AM và trọng tâm G. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE = CF.
a) Chứng minh G là trọng tâm tam giác AEF.
b) Gọi N là trung điểm của AF. Chứng minh ba điểm E, G, N thẳng hàng.
c) Gọi H là trung điểm của GA, I là trung điểm GE. Chứng minh IH // MN và IH = MN.
Cho tam giác ABC có ABAC, M là trung điểm của BC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy E sao cho AD AEa. Chứng minh rằng tâm giác AMB tam giác AMCb. Chứng minh rằng AM là tia phân giác của góc A và AM vuông góc với BCc. Gọi K là giao điểm của AM và DE. Chưng minh AK vuông góc với DEd. trên tia đối của tia ED lấy đeiểm F sao cho FE MC, gọi H là trung điểm của EC. Chứng minh 3 điểm M, H, F thẳng hàng
Đọc tiếp
Cho tam giác ABC có AB=AC, M là trung điểm của BC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy E sao cho AD= AE
a. Chứng minh rằng tâm giác AMB = tam giác AMC
b. Chứng minh rằng AM là tia phân giác của góc A và AM vuông góc với BC
c. Gọi K là giao điểm của AM và DE. Chưng minh AK vuông góc với DE
d. trên tia đối của tia ED lấy đeiểm F sao cho FE= MC, gọi H là trung điểm của EC. Chứng minh 3 điểm M, H, F thẳng hàng
Cho tam giác ABC , điểm D thuộc cạnh BC . Gọi M là trung điểm của AD . Trên tia đối của tia MB lấy điểm E sao cho ME=MB . Trên tia đối của tia MC lấy điểm F sao cho MF=Mc . chứng minh :
a) AE=BD
b) AF//BC
c) Ba điểm A, E, F thẳng hàng
Cho tam giác ABC, điểm D thuộc cạnh BC. Gọi M là trung điểm của AD. Trên tia đối của tia MB lấy điểm E sao cho ME = MB. Trên tia đối của tia MC lấy F sao cho MF = MC. Chứng minh:
a) AE = BD;
b) AF // BC.
c) Ba điểm A, E, F thẳng hàng.
Bài 1. Cho góc xOy, có Ot là tia phân giác. Lấy điểm A trên tia Ox, điểm B trên tia Oy sao cho OA OB. Vẽ đoạn thẳng AB cắt Ot tại M. Chứng minh
a) OAM OBM;
b) AM BM; OM AB
c) OM là đường trung trực của AB
d) Trên tia Ot lấy điểm N . Chứng minh NA NB
Bài 2. Cho ABC vuông tại A, trên tia đối của tia CA lấy điểm K sao cho CK CA, từ K kẻ KE vuông góc với đường thẳng AC. Chứng mỉnhằng:
a) AB // KE b) ABC KEC ; BC CE
Bài 3. Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C....
Đọc tiếp
\(Bài 1. Cho góc xOy, có Ot là tia phân giác. Lấy điểm A trên tia Ox, điểm B trên tia Oy sao cho OA = OB. Vẽ đoạn thẳng AB cắt Ot tại M. Chứng minh a) OAM = OBM; b) AM = BM; OM AB c) OM là đường trung trực của AB d) Trên tia Ot lấy điểm N . Chứng minh NA = NB Bài 2. Cho ABC vuông tại A, trên tia đối của tia CA lấy điểm K sao cho CK = CA, từ K kẻ KE vuông góc với đường thẳng AC. Chứng mỉnhằng: a) AB // KE b) ABC = KEC ; BC = CE Bài 3. Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C. Trên tia Oy lấy hai điểm B,D sao cho OA = OB, AC = BD. a) Chứng minh: AD = BC. b) Gọi E là giao điểm AD và BC. Chứng minh: EAC = EBD c) Chứng minh: OE là phân giác của góc xOy, OE CD Bài 4. Cho ABC coù BÂ=900, gọi M là trung điểm của BC. Trên tia đối của tia AM lấy điểm E sao cho ME = MA. a) Tính BCE b) Chứng minh BE // AC. Bài 5. Cho ABC, lấy điểm D thuộc cạnh BC ( D không trùng với B,C). Gọi Mlà trung điểm của AD. Trên tia đối của tia MB lấy điểm E sao cho ME= MB, trên tia đối của tia MC lấy điểm F sao cho MF= MC. Chứng minh rằng: a) AME = DMB; AE // BC b) Ba điểm E, A, F thẳng hàng c) BF // CE Bài 6: Cho có B = C , kẻ AH BC, H BC . Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh: a) AB = AC b) ABD = ACE c) ACD = ABE d) AH là tia phân giác của góc DAE e) Kẻ BK AD, CI AE. Chứng minh ba đường thẳng AH, BK, CI cùng đi qua một điểm. \)