Các câu hỏi tương tự
Cho △ABC, trên nửa mặt phẳng bờ AC không chứa điểm B, lấy điểm D sao cho AC // BC và AD = BC. Chứng minh:
a) △ABC = △CDA
b) AB // CD và △ABD = △CDB
#Có vẽ hình#
Cho ∆ A B C , trên nửa mặt phẳng bờ AC không chứa điểm B, lấy điểm D sao cho AD//BC và AD = BC. Chứng minh:
a) ∆ A B C = ∆ C D A .
b) AB //CD và ∆ A B D = ∆ C D B .
Cho tam giác ABC nhọn. Trên nửa mặt phẳng bờ AC không chứa B, lấy D sao cho AC song song BC và AD=BC. Gọi O là giao của AC và BD
Chứng minh:
a) tam giác ABC= tam giác CDA
b) tam giác ABD= tam giác CDB
c) tam giác OBC= tam giác ODA
Cho tam giác ABC nhọn. Trên nửa mặt phẳng bờ AB, không chứa điểm C, lấy điểm D sao cho AD vuông góc AB; AD=AB. Trên nửa mặt phẳng bờ AC, không chứa điểm B, lấy điẻm E sao cho AE vuông góc AC; AE=AC. Kẻ AH vuông góc BC, tia HA cắt DE tại K. Chứng minh rằng K là trung điểm của DE.
Cho tam giác ABC nhọn. Trên nửa mặt phẳng bờ AB, không chứa điểm C, lấy điểm D sao cho AD vuông góc AB; AD=AB. Trên nửa mặt phẳng bờ AC, không chứa điểm B, lấy điẻm E sao cho AE vuông góc AC; AE=AC. Kẻ AH vuông góc BC, tia HA cắt DE tại K. Chứng minh rằng K là trung điểm của DE
Cho tam giác ABC. Trên nửa mặt phẳng không chứa điểm C có bờ là đường thẳng AB, vẽ tia AD sao cho
B
A
D
^
A
B
C
^
. Trên nửa mặt phẳng không chứa điểm B có bờ là đường thẳng AC, vẽ tia AE sao cho
C
A
E
^
A
C
B...
Đọc tiếp
Cho tam giác ABC. Trên nửa mặt phẳng không chứa điểm C có bờ là đường thẳng AB, vẽ tia AD sao cho B A D ^ = A B C ^ . Trên nửa mặt phẳng không chứa điểm B có bờ là đường thẳng AC, vẽ tia AE sao cho C A E ^ = A C B ^ . Chứng minh.:
a) AD song song với BC;
b) Ba điểm D, A, E thẳng hàng
Cho tam giác ABC. Trên nửa mặt phẳng không chứa điểm C có bờ là đường thẳng AB, vẽ tia AD sao cho
B
A
D
^
A
B
C
^
. Trên nửa mặt phẳng không chứa điểm B có bờ là đường thẳng AC, vẽ tia AE sao cho
C
A
E
^...
Đọc tiếp
Cho tam giác ABC. Trên nửa mặt phẳng không chứa điểm C có bờ là đường thẳng AB, vẽ tia AD sao cho B A D ^ = A B C ^ . Trên nửa mặt phẳng không chứa điểm B có bờ là đường thẳng AC, vẽ tia AE sao cho C A E ^ = A C B ^ . Chứng minh.:
a) AD song song với BC;
b) Ba điểm D, A, E thẳng hàng
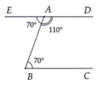
Cho tam giác ABC có AB=AC. Trên nửa mặt phẳng bờ BC không chứa A, vẽ tam giác CDB sao cho DC=DB. Chứng minh AD vuông góc BC. CHỈ SỬ DỤNG TRƯỜNG HỢP CẠNH-CẠNH-CẠNH
Cho tam giác AB nhọn. Trên nửa mặt phẳng bờ ABD, không chứa điểm D, lấy điểm C sao cho AC vuông góc AB; AC=AB. Trên nửa mặt phẳng bờ D, không chứa điểm B, lấy điẻm E sao cho AE vuông góc AD; AE=AD. Kẻ AH vuông góc BC, tia HA cắt CE tại K. Chứng minh rằng K là trung điểm của CE.







