Các câu hỏi tương tự
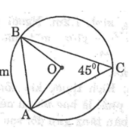
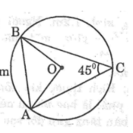
cho tam gíc ABC nội tiếp đường tròn (O) bán kính R có góc C = 45 độ
a. tính diện tích hình quạt tròn AOB (ứng với cung nhỏ AB)
b. tính diện tích hình viên phân AmB (ứng với cung nhỏ AB)
Cho tam giác ABC nội tiếp trong đường tròn (O;R) có góc C = 45 ° . Tính diện tích hình quạt tròn AOB(ứng với cung nhỏ AB)
1. Cho tam giác ABC có A 60o nội tiếp trong đường tròn (O;R)a) tính số đo cung BCb) tính độ dài dây cung BC và độ dài cung BC theo Rc) tính diện tích hình quạt ứng với góc ở tâm BOC theo R2. CHo (O;R) và dây AB Rsqrt{2}a) tính số đo cung AB, số đo góc AOBb)| tính theo R độ dài cung ABtính diện tích của hình viên phân giới hạn bởi dây AB và cung nhỏ AB theo R
Đọc tiếp
1. Cho tam giác ABC có A= 60o nội tiếp trong đường tròn (O;R)
a) tính số đo cung BC
b) tính độ dài dây cung BC và độ dài cung BC theo R
c) tính diện tích hình quạt ứng với góc ở tâm BOC theo R
2. CHo (O;R) và dây AB= R\(\sqrt{2}\)
a) tính số đo cung AB, số đo góc AOB
b)| tính theo R độ dài cung AB
tính diện tích của hình viên phân giới hạn bởi dây AB và cung nhỏ AB theo R
Từ điểm M nằm ngoài đường tròn tâm O, kẻ 2 tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Giả sử góc AMB = 60 độ, tính diện tích hình viên phân giới hạn bởi dây AB và cung nhỏ AB theo R.
cho tam giác ABC nội tiếp đường tròn (O;R), BC= Rcan3. M là điểm bất kì trên cung nhỏ BC. Gọi D,E,F lần lượt là hình chiếu của M lên AB,BC,CA.
a) Chứng minh 4 điểm B,D,E,M cùng thuộc một đường tròn
b) Tính diện tích hình viên phân tạo bởi cung nhỏ BC
Bạn nào giúp mình với được không ạ huhu :<
1. Cho nửa đường tròn ( O ; R ) có đường kính là AB. Vẽ dây CD = R ( C thuộc cung AD ) . Nối AC và BD cắt tại M
a. Cm : tam giác MCD đồng dạng với tam giác MBA
b. Cho góc ABC = 30. Tính theo R cung nhỏ AC và diện tích viên phân giới hạn bởi dây AC và cung nhỏ AC.
c. Khi CD // AB. Tính diện tích tam giác MCD.
Cho tam giác ABC nhọn nội tiếp (O;R) AB < AC, các đường cao BD, CE
a, Chứng minh BEDC nội tiếp
b, Qua A vẽ tiếp tuyến xy với (O). Chứng minh xy // ED
c, Chứng minh góc EBD = góc ECD
d. Kẻ OH vuông góc BC. Cho góc BAC = 60o, R = 2 cm. Tính diện tích hình viên phân tạo bởi cung nhỏ BC và dây căng cung đó.
Cho nửa đường tròn (O; R) đường kính AB. Vẽ dây CD R (C thuộc cung AD). Nối AC và BD cắt nhau tại Ma, Chứng minh rằng khi CD thay đổi vị trí trên nửa đường tròn thì độ lớn góc
A
M
B
^
không đổib, Cho
A
B
C
^
30...
Đọc tiếp
Cho nửa đường tròn (O; R) đường kính AB. Vẽ dây CD = R (C thuộc cung AD). Nối AC và BD cắt nhau tại M
a, Chứng minh rằng khi CD thay đổi vị trí trên nửa đường tròn thì độ lớn góc A M B ^ không đổi
b, Cho A B C ^ = 30 0 , tính độ dài cung nhỏ AC và diện tích hình viên phân giói hạn bởi dây AC và cung nhỏ AC
Cho tam giác ABC nội tiếp trong nửa đường tròn tâm O đường kính AB2R. Lấy H là trung điểm của dây BC.Tia OH cắt đường tròn tại D. Tia AC, AD lần lượt cắt tiếp tuyên Bx của nửa đường tròn tại E và Fa/ Chứng minh AD là tia phân giác của góc ACBb/ Chứng minh tứ giác ECDF là tứ giác nội tiếpc/ Cho CD R. Tính diện tích của hình viên phân giới hạn bởi cung CDB với dây CBGIÚP MÌNH CÂU B,C NHÉ, THANKS
Đọc tiếp
Cho tam giác ABC nội tiếp trong nửa đường tròn tâm O đường kính AB=2R. Lấy H là trung điểm của dây BC.Tia OH cắt đường tròn tại D. Tia AC, AD lần lượt cắt tiếp tuyên Bx của nửa đường tròn tại E và F
a/ Chứng minh AD là tia phân giác của góc ACB
b/ Chứng minh tứ giác ECDF là tứ giác nội tiếp
c/ Cho CD= R. Tính diện tích của hình viên phân giới hạn bởi cung CDB với dây CB
GIÚP MÌNH CÂU B,C NHÉ, THANKS