Hướng dẫn làm bài:
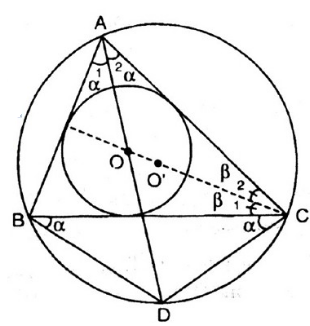
Vì AC vad BC tiếp xúc với đường tròn (O), AD đi qua O nên ta có:
ˆCAD=ˆBAD=αCAD^=BAD^=α (vì tâm đường tròn nội tiếp trong tam giác là giao điểm của ba đường phân giác trong tam giác)
⇒ cung CD = cung DB ⇒CD = DB (*)
Tương tự, CO là tia phân giác của góc C nên:
ˆACO=ˆBCO=βACO^=BCO^=β
Mặt khác: ˆDCO=ˆDCB+ˆBCO=α+β(1)(doˆBAD=ˆBCDDCO^=DCB^+BCO^=α+β(1)(doBAD^=BCD^
Ta có: ˆCODCOD^ là góc ngoài của ∆ AOC nên
ˆCOD=ˆOAC+ˆOCA=β+α(2)COD^=OAC^+OCA^=β+α(2)
Từ (1) và (2) ta có: ˆOCD=ˆCODOCD^=COD^
Vậy ∆DOC cân tại D (**)
Từ (*) và (**) suy ra CD = OD = BD
Chọn đáp án D
Đúng 0
Bình luận (0)
