a,Chứng minh được BFCH là hình bình hành
b, Sử dụng kết quả câu a), suy ra HF đi qua M
c, Chú ý: OM là đường trung bình của ∆AHF => ĐPCM

a,Chứng minh được BFCH là hình bình hành
b, Sử dụng kết quả câu a), suy ra HF đi qua M
c, Chú ý: OM là đường trung bình của ∆AHF => ĐPCM
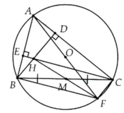
Cho tam giác ABC nhọn nội tiếp đường tròn (O). 2 đường cao BD, CE cắt nhau tại H . Vẽ đường kính AF
a) BFCH là hình gì ? cm
b) gọi M là trung điểm BC. cm : M,H,F thẳng hàng
c) cm: AH = 2.OM
Cho tam giác ABC nhọn nội tiếp đường tròn (O). 2 đường cao BD, CE cắt nhau tại H . Vẽ đường kính AF
a) BFCH là hình gì ? cm
b) gọi M là trung điểm BC. cm : M,H,F thẳng hàng
c) cm: AH = 2.OM
Cho tam giác ABC nhọn nội tiếp đường tròn O. Các đường cao AI, BK cắt nhau tại H. Vẽ đường kính CD.
a) Tứ giác ADBK là hình gì?
b) Gọi M là trung điểm AB. Chứng minh OM vuông góc AB và OM song song CH
c) Chứng minh ba điểm H, M, D thẳng hàng
Cho tam giác ABC. Hai đường cao BE, CF cắt nhau tại H. Gọi M và O lần lượt là trung điểm của AH, BC. Chứng minh rằng
a, AFHE là tứ giác nội tiếp
b, OE là tiếp tuyến của đường tròn đường kính AH
c, OE cắt AH tại S. Chứng minh rằng SE2=SH.SA
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Hai đường cao BD, CE của tam giác ABC cắt nhau tại H. a) Chứng minh tứ giác BFEC nội tiếp được một đường tròn. b) Kẻ đường kính AD của đường tròn (O). Tứ giác BFCD là hình gì? Vì sao? c) Gọi M là trung điểm của BC. Chứng minh AH = 2OM. d) Chứng minh OA | EF
Làm giúp mình 2 bài này với, mai mình phải nộp rồi!!!
Bài 1:
Từ điểm A nằm ngoài đường tròn (O;R), vẽ 2 tiếp tuyến AB, AC với đường tròn.
a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc BC tại H
b) Vẽ đường kính CD của đường tròn (O;R), AD cắt (O) tại M. Chứng minh: góc BHM = góc MAC
c) Tia BM cắt AO tại N. Chứng minh NA=NH
d) Vẽ ME là đường kính đường tròn (O), gọi I là trung điểm DM. Chứng minh: 3 điểm B, I, E thẳng hàng và BI song song MH.
Bài 2:
Cho tam giác ABC vuông tại A. Vẽ đường tròn tâm O đường kính AC cắt BC tại H. Gọi I là trung điểm của HC. Tia OI cắt (O) tại F
a) Chứng minh AH là đường cao của tam giác ABC và AB^2= BH. BC
b) Chứng minh: Tứ giác ABIO nội tiếp
c) Chứng minh: AF là tia phân giác của góc HAC
d) AF cắt BC tại D. Chứng minh: BA=BD
Cho tam giác ABC nhọn (AB < AC). Đường tròn (O) đường kính BC cắt AB và AC lần lượt tại E và D. Gọi H là giao điểm của BD và CE . Tia AH cắt BC tại F.
a) Chứng minh: HB . HD = HC . HE và AF vuông góc với BC.
b) Gọi M là trung điểm của CH. Chứng minh tứ giác OMEF là tứ giác nội tiếp.
c) Đoạn thẳng DF cắt CE tại N . Qua N vẽ đường thẳng vuông góc với CE cắt BC và BD lần lượt tại I và K . Chứng minh N là trung điểm của IK
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O có hai đường cao là BD và CE giao nhau tại H. Vẽ đường kính AK của đường tròn tâm O.
a) Chứng minh: tứ giác BHCK là hình bình hành
b) OM vuông góc với BC tại M. Chứng minh \(OM=\frac{1}{2}AH\)
Giúp em với mọi người
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O (AB<AC) Hai đường cao AD, CE cắt nhau tại H
a. Kẻ đường kính AK cắt CE tại M, CK cắt AD tại F, chứng minh tứ giác BEHD nội tiếp và AH. AF= AM.AK
b. Gọi I là trung điểm của BC, EI cắt AK tại N, Chứng minh tứ giác EDNC là hình thang cân