Question

Cho tam giác ABC nhọn(AB<AC) và nội tiếp (O).Vẽ phân giác AD của góc BAC (D ), AD cắt (O) tại M ( M khác A). Chứng minh : MC²  =MD.MA

Answer 1

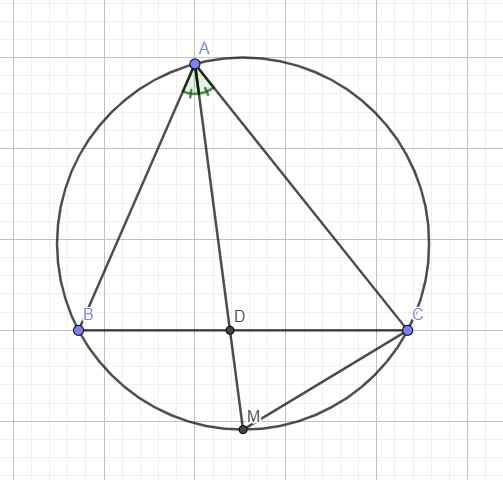
Do AD là phân giác \(\Rightarrow\widehat{BAM}=\widehat{CAM}\)

Mà \(\widehat{BAM}=\widehat{BCM}\) (cùng chắn cung BM)

\(\Rightarrow\widehat{CAM}=\widehat{BCM}\) 

Xét hai tam giác ACM và CDM có:

\(\left\{{}\begin{matrix}\widehat{AMC}\text{ chung}\\\widehat{CAM}=\widehat{BCM}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta ACM\sim\Delta CDM\left(g.g\right)\)

\(\Rightarrow\dfrac{AM}{CM}=\dfrac{CM}{DM}\Rightarrow CM^2=MA.MD\) (đpcm)

Answer 2

Answer 3

Ta có : ^BAM = ^MAC ( AD là phân giác ) 

^BAM = ^BCM ( góc nt chắn cung MB ) 

=> ^BCM = ^MAC 

Xét tam giacs MCD và tam giác MAC có : 

^M _ chung 

^BCM = ^CAM (cmt) 

Vậy tam giác MCD ~ tam giác MAC (g.g)

=> MC/MA=MD/MC => MC^2 = MD.MA