Question

Cho tam giác ABC nhọn , vẽ đường cao AH, về phía ngoài của tam giác vẽ các tam giác vuông cân ABE và ACF vuông ở B và C. Trên tia đối của AH lấy điểm I sao cho AI= BC. Chứng minh rằng:

a, Tam giác ABI= Tam giác BEC

b, BI=CE và BI vuông góc với CE

c, 3 đường thẳng AH, CE và BF cắt nhau tại 1 điểm

Answer 1

Hình vẽ:

Answer 2

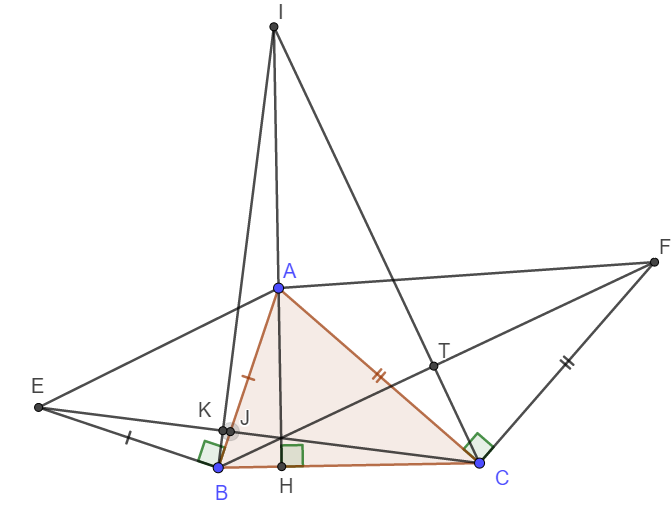
a) Ta có  \(\widehat{AHB}=90^o\)

Theo tính chất góc ngoài của tam giác, ta có:

\(\widehat{IAB}=\widehat{AHB}+\widehat{HBA}=90^o+\widehat{HBA}=\widehat{EBA}+\widehat{HBA}=\widehat{CBE}\)

Xét tam giác ABI và tam giác BEC có:

AI = BC (gt)

BA = EB (gt)

\(\widehat{IAB}=\widehat{CBE}\)  (cmt)

\(\Rightarrow\Delta ABI=\Delta BEC\left(c-g-c\right)\)

b) Do \(\Delta ABI=\Delta BEC\Rightarrow BI=EC\)

Gọi giao điểm của EC với AB và BI lần lượt là J và K.

Do \(\Delta ABI=\Delta BEC\Rightarrow\widehat{KBJ}=\widehat{BEK}\)

Vậy thì \(\widehat{KBJ}+\widehat{KJB}=\widehat{BEK}+\widehat{KJB}=90^o\)

Suy ra \(\widehat{BKJ}=90^o\) hay \(BI\perp CE\)

c) Chứng minh hoàn toàn tương tự ta có \(IC\perp BF\)

Gọi giao điểm của IC và BF là T.

Xét tam giác IBC có IH, CK, BT là các đường cao nên chúng đồng quy tại một điểm.

Vậy AH, EC, BF đồng quy tại một điểm.

Answer 3

em chào các thầy

Answer 4

Cô ơi em muốn hỏi làm thế nào để cm IC \(\perp\)BF ạ?

Answer 5

Ai sợ thì đi về