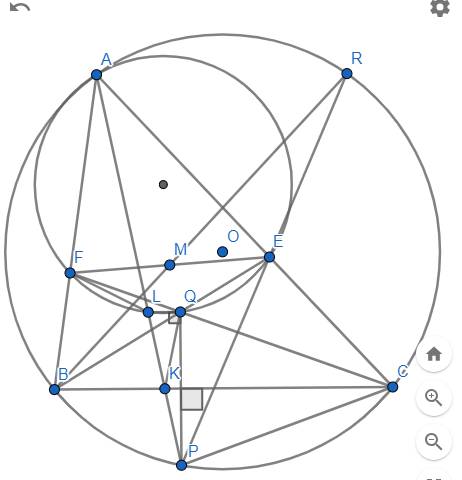
: Cho tam giác ABC nhọn, nội tiếp (O). P thuộc cung nhỏ BC. AP cắt BC tại K. Q đối xứng với P qua BC sao cho Q nằm trong tam giác ABC. BQ cắt AC tại E. CQ cắt AB tại F.
a) Chứng minh: BKQF, KQEC nội tiếp
b) CMR: AF QE là tứ giác nội tiếp
c) AK cắt (AEF) tại L. Chứng minh: PQL=90 độ
d) P E cắt (O) tại R. BR cắt EF tại M. Chứng minh: ME = MF.
(a) \(P,Q\) đối xứng với nhau qua \(BC\) nên \(BC\) là đường trung trực của \(PQ\).
Suy ra: \(CQ=CP\Rightarrow\Delta CPQ\) cân tại \(C\Rightarrow\hat{KCP}=\hat{KCQ}\), hay \(\hat{BCP}=\hat{BCF}\). Mà \(\hat{BAP}=\hat{BCP}\) (góc nội tiếp cùng chắn cung \(\stackrel\frown{BP}\)).
Do đó: \(\hat{BAP}=\hat{BCF}\)
Xét \(\Delta ABK,\Delta CBF:\)
\(\hat{B}\) chung và \(\hat{BAP}=\hat{BCF}\left(cmt\right)\)
\(\Rightarrow\Delta ABK\sim\Delta CBF\left(g.g\right)\Rightarrow\dfrac{AK}{CF}=\dfrac{AB}{CB}\Leftrightarrow\dfrac{AK}{AB}=\dfrac{CF}{CB}\left(1\right)\)
Ta cũng dễ chứng minh được \(\Delta ABK\sim\Delta CPK\left(g.g\right)\Rightarrow\dfrac{AK}{CK}=\dfrac{AB}{CP}=\dfrac{AB}{CQ}\left(CP=CQ\left(cmt\right)\right)\)
\(\Rightarrow\dfrac{AK}{AB}=\dfrac{CK}{CQ}\left(2\right)\).
Từ (1) và (2), suy ra: \(\dfrac{CF}{CB}=\dfrac{CK}{CQ}\Leftrightarrow\dfrac{CQ}{CB}=\dfrac{CK}{CF}\).
Xét \(\Delta CQK,\Delta CBF:\left\{{}\begin{matrix}\hat{C}\text{ chung}\\\dfrac{CQ}{CB}=\dfrac{CK}{CB}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta CQK\sim\Delta CBF\left(c.g.c\right)\Rightarrow\hat{CKQ}=\hat{CFB}\).
Lại có: \(\hat{CKQ}+\hat{QKB}=180^o\) (kề bù), suy ra \(\hat{CFB}+\hat{QKB}=180^o\).
Đây là hai góc đối nhau nên tứ giác \(BKQF\) nội tiếp được một đường tròn (đpcm).
Chứng minh tương tự như trên thì ta cũng suy ra được tứ giác \(KQEC\) nội tiếp được một đường tròn.
(b) Từ câu a, \(KQEC\) là tứ giác nội tiếp nên \(\hat{QEA}=\hat{QKC}\) (cùng bù với \(\hat{QEC}\)); \(BFQK\) là tứ giác nội tiếp nên \(\hat{QFB}=\hat{QKC}\) (cùng bù với \(\hat{QKB}\)).
Suy ra: \(\hat{QFB}=\hat{QEA}\).
Lại có: \(\hat{QFB}+\hat{QFA}=180^o\) (kề bù) nên \(\hat{QEA}+\hat{QFA}=180^o\)
Đây là hai góc đối nhau nên tứ giác \(AFQE\) nội tiếp (đpcm).
(c) \(L\in\left(AEF\right)\) mà tứ giác \(AFQE\) nội tiếp (cmt), suy ra \(Q\in\left(AEF\right)\), hay tứ giác \(AFLQ\) nội tiếp.
Suy ra: \(\hat{FAL}=\hat{FQL}\) (hai góc cùng nhìn một cạnh), hay \(\hat{BAP}=\hat{FQL}\).
Mà ở câu a, \(\hat{BAP}=\hat{BCF}\Rightarrow\hat{BAP}=\hat{KCQ}\).
\(\Rightarrow\hat{KCQ}=\hat{FQL}\).
Hai góc này ở vị trí đồng vị nên \(QL\left|\right|CK\), mà \(CK\perp PQ\) (\(BC\) là đường trung trực của \(PQ\) (chứng minh ở a))
Do đó, \(QL\perp PQ\), tức \(\hat{PQL}=90^o\left(đpcm\right)\)