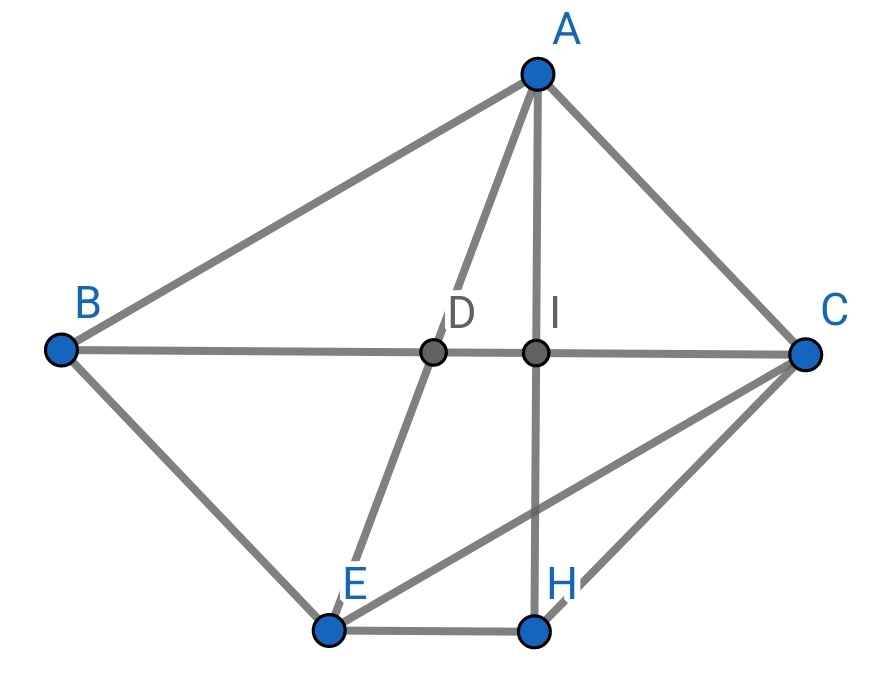
a) Do A và E đối xứng qua D
⇒D là trung điểm AE
Tứ giác ABEC có:
D là trung AE (cmt)
D là trung điểm BC (gt)
⇒ABEC là hình bình hành
b) Do A và H đối xứng qua BC
⇒BC là đường trung trực của AH
⇒I là trung điểm AH và AH vuông góc BC
⇒AH vuông góc DI
∆AEH có:
D là trung điểm AE (cmt)
I là trung điểm AH (cmt)
⇒DI là đường trung bình của ∆AEH
⇒DI // EH
Mà DI vuông góc AH
⇒AH vuông góc EH
c) Do DI // EH
⇒BC // EH
⇒BCHE là hình thang (1)
Ta có:
ABEC là hình bình hành (cmt)
⇒BE // AC
⇒góc EBC = góc ACB (so le trong) (2)
Xét hai tam giác vuông: ∆AIC và ∆HIC có:
AI chung
AI = HI (I là trung điểm AH)
⇒∆AIC = ∆HIC (hai cạnh góc vuông)
⇒góc ACI = góc HCI (hai góc tương ứng)
⇒góc ACB = góc HCB (3)
Từ (2) và (3) ⇒góc HCB = góc EBC (4)
Từ (1) và (4) ⇒BCHE là hình thang cân










