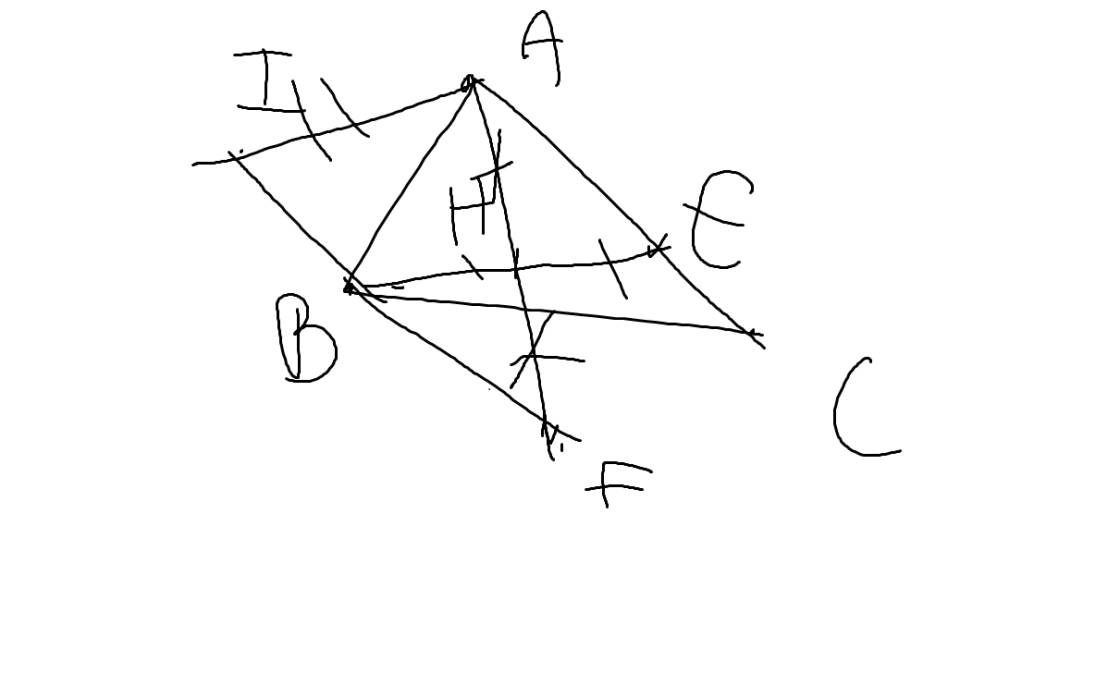
Cho tam giác ABC nhọn có AB<AC. Trên cạnh AC lấy E sao cho AB=AE. Gọi H là trung điểm BE. 1) Chứng minh tam giác ABH=AEH (c.c.c) 2) Chứng minh AH vuông góc BE 3) Trên AH lấy điểm F sao AH=HF. Kẻ Ax // BC. Trên Ax lấy I sao AI=BE (I cùng phía với AH). Chứng minh rằng: a) Chứng minh BF=AE b) Chứng minh 3 điểm I, B, F thẳng hàng ( kẻ hình nữa nhé )
cảm ơn các bạn nhiều , lm nhanh nhất có thể giúp mik nhé ![]()
1: Xét ΔABH và ΔAEH có
AB=AE
BH=EH
AH chung
Do đó: ΔAHB=ΔAHE
2: ΔAHB=ΔAHE
=>\(\widehat{AHB}=\widehat{AHE}\)
mà \(\widehat{AHB}+\widehat{AHE}=180^0\)(hai góc kề bù)
nên \(\widehat{AHB}=\widehat{AHE}=\dfrac{180^0}{2}=90^0\)
=>AH\(\perp\)BE
3: Sửa đề: Kẻ tia Ax//BE, trên Ax lấy I sao cho AI=BE(I và B nằm cùng phía so với AH)
a: Xét tứ giác ABFE có
H là trung điểm chung của AF và BE
=>ABFE là hình bình hành
=>BF=AE và BF//AE
b:
Xét tứ giác AEBI có
AI//BE
AI=BE
Do đó: AEBI là hình bình hành
=>BI//AE
Ta có: BF//AE
BI//AE
BI,BF có điểm chung là B
Do đó: F,B,I thẳng hàng