Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Tam giác ABC có \(A=120^o\) thì khẳng định nào sau đây là đúng?
A. a^2 = b ^ 2 + c ^ 2 - bc
B. a^2 = b^2 + c^2 + 3bc
C. a^2 = b^2 + c^2 + bc
D. a^2 = b^2 + c^2 - 3bc
( ^2 có nghĩa là bình phương )
Cho tam giác ABC có A(1; -2; 3), B(0; 5; 6), C(1; 3; 2). Gọi H là hình chiếu vuông góc của A trên đường thẳng BC. Trong những khẳng định dưới đây, khẳng định nào sai? A. Một vectơ pháp tuyến của mặt phẳng (ABC) là: B. Một vectơ chỉ phương của đường thẳng AH là: C. AH ⊥ BC D. Các khẳng định trên không đồng thời đúng
Đọc tiếp
Cho tam giác ABC có A(1; -2; 3), B(0; 5; 6), C(1; 3; 2). Gọi H là hình chiếu vuông góc của A trên đường thẳng BC. Trong những khẳng định dưới đây, khẳng định nào sai?
A. Một vectơ pháp tuyến của mặt phẳng (ABC) là: ![]()
B. Một vectơ chỉ phương của đường thẳng AH là: ![]()
C. AH ⊥ BC
D. Các khẳng định trên không đồng thời đúng
Trong không gian Oxyz, cho ba điểm A(0; 0; 0), B(1; 2; 3), C(2; 3; 1). Gọi D là chân đường phân giác trong xuất phát từ đỉnh A của tam giác ABC. Trong các khẳng định dưới đây, khẳng định nào sai? A. AD ⊥ BC B. Một vectơ chỉ phương của đường thẳng AD là:
AB
→
+
AC
→
C. Một vectơ chỉ phương của đường thẳng AD là: D. Một vectơ chỉ phương của đường thẳng AD là: ...
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A(0; 0; 0), B(1; 2; 3), C(2; 3; 1). Gọi D là chân đường phân giác trong xuất phát từ đỉnh A của tam giác ABC. Trong các khẳng định dưới đây, khẳng định nào sai?
A. AD ⊥ BC
B. Một vectơ chỉ phương của đường thẳng AD là: AB → + AC →
C. Một vectơ chỉ phương của đường thẳng AD là: 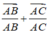
D. Một vectơ chỉ phương của đường thẳng AD là: u AD → = (1; 1; -2)
Cho ba điểm A(4; 3), B(2; 7) và C(-3; -8).
a, Tìm tọa độ trọng tâm G và trực tâm H của tam giác ABC;
b, Gọi T là tâm đường tròn ngoại tiếp tam giác ABC. Chứng minh T, G và H thẳng hàng.
c, Viết phương trình đường tròn ngoại tiếp tam giác ABC.
Cho tam giác ABC với A(1; 4), B(3; -2), C(4; 5) và đường thẳng ∆: 2x – 5y + 3 = 0. Khẳng định nào sau đây là đúng?
A. Đường thẳng ∆ không cắt cạnh nào của tam giác
B. Đường thẳng ∆ cắt 1 cạnh của tam giác
C. Đường thẳng ∆ cắt 2 cạnh của tam giác
D. Đường thẳng ∆ cắt 3 cạnh của tam giác
Cho tam giác ABC có A(1; 3; 5), B(-4; 0; -2), C(3; 9; 6). Gọi G là trọng tâm tam giác ABC. Trong những khẳng định dưới đây, khẳng định nào sai? A. Tọa độ của điểm G là (0;4;3) B. AG ⊥ BC C. Phương trình tham số của đường thẳng OG là: x 0, y 4t, z 3t D. Đường thẳng OG nằm trong hai mặt phẳng: (P): x 0, (Q): 3y - 4z 0
Đọc tiếp
Cho tam giác ABC có A(1; 3; 5), B(-4; 0; -2), C(3; 9; 6). Gọi G là trọng tâm tam giác ABC. Trong những khẳng định dưới đây, khẳng định nào sai?
A. Tọa độ của điểm G là (0;4;3)
B. AG ⊥ BC
C. Phương trình tham số của đường thẳng OG là: x = 0, y = 4t, z = 3t
D. Đường thẳng OG nằm trong hai mặt phẳng: (P): x = 0, (Q): 3y - 4z = 0
Cho điểm A(-1;1) B(3;2) C(-1/2;1)
a)Chứng minh :3điểm A B C không thẳng hàng. Tính chu vi tam giác ABC
b)Chứng minh :Tam giác ABC vuông. Tìm tâm đường tròn ngoại tiếp tam giác ABC c)Tìm D thuộc OY.Tam giác ABC vuông tại D
d)Tìm M sao cho MA^2+MB^2+MO^2 nhỏ nhất
Cho tam giác ABC. Chứng minh rằng:a) Nếu (a+b+c).(b+c-a)3bc thì widehat{A}60^ob) Nếu frac{b^3+c^3-a^3}{b+c-a}a2 thì widehat{A}60^oc) Nếu cos.(A+C)+3.cosB1 thì widehat{B}60^od) Nếu b.(b2-a2)c.(a2-c2) thì widehat{A}60^o
Đọc tiếp
Cho tam giác ABC. Chứng minh rằng:
a) Nếu (a+b+c).(b+c-a)=3bc thì \(\widehat{A}=60^o\)
b) Nếu \(\frac{b^3+c^3-a^3}{b+c-a}\)=a2 thì \(\widehat{A}=60^o\)
c) Nếu cos.(A+C)+3.cosB=1 thì \(\widehat{B}=60^o\)
d) Nếu b.(b2-a2)=c.(a2-c2) thì \(\widehat{A}=60^o\)
Cho tam giác ABC có diện tích là S. BC = a, AC = b, AB = c. G là trọng tâm tam giác. Chứng minh rằng:
a/ \(cotA=\dfrac{b^2+c^2-a^2}{4S}\)
b/ \(cotA+cotB+cotC=\dfrac{a^2+b^2+c^2}{4S}\)
c/ \(GA^2+GB^2+GC^2=\dfrac{1}{3}\left(a^2+b^2+c^2\right)\)
d/ \(b^2-c^2=a\left(b.cosC-c.cosB\right)\)
Cho tam giác ABC có A(1; 2), B(–2; 6), C(9; 8).a Tính . Cm tam giác ABC vuông tại A.b Tìm tâm và bán kính đường tròn ngoại tiếp tam giác ABC.c Tìm toạ độ trực tâm H và trọng tâm G của tam giác ABC.d Tính chu vi, diện tích tam giác ABC.e Tìm toạ độ điểm M trên Oy để B, M, A thẳng hàng.f Tìm toạ độ điểm N trên Ox để tam giác ANC cân tại N.g Tìm toạ độ điểm D để ABDC là hình chữ nhật.h Tìm toạ độ điểm K trên Ox để AOKB là hình thang đáy AO.
Đọc tiếp
Cho tam giác ABC có A(1; 2), B(–2; 6), C(9; 8).
a Tính . Cm tam giác ABC vuông tại A.
b Tìm tâm và bán kính đường tròn ngoại tiếp tam giác ABC.
c Tìm toạ độ trực tâm H và trọng tâm G của tam giác ABC.
d Tính chu vi, diện tích tam giác ABC.
e Tìm toạ độ điểm M trên Oy để B, M, A thẳng hàng.
f Tìm toạ độ điểm N trên Ox để tam giác ANC cân tại N.
g Tìm toạ độ điểm D để ABDC là hình chữ nhật.
h Tìm toạ độ điểm K trên Ox để AOKB là hình thang đáy AO.









