Chọn C.
Sử dụng công thức hạ bậc và biến đổi tổng thành tích ta có :
cos2A + cos2B + cos2C 
= 1 + cos( A + B) .cos( A – B) + cos2C = 1 – cos C. cos( A – B) – cos C.cos( A + B)
= 1 – cosC[cos (A - B) + cos(A + B) ] = 1 + 2cosA. cosB.cosC
cho tam giác ABC chứng minh: cos2A + cos2B + cos2C = -1 - 4cosA.cosB.cosC
Cho các góc lượng giác a, b thỏa mãn cos 2 a + cos 2 b = m m ∈ ℝ . Giá trị của biểu thức P = cos a + b . cos a - b là
A. P = m 2 - 1
B. P = 1 - m 2
C. P = m - 1
D. P = m + 1
Cho tam giác ABC thỏa mãn: cos 2 A + cos 2 B sin 2 A + sin 2 B = 1 2 ( c o t 2 A + c o t 2 B ) Tìm mệnh đề đúng?
A. Tam giác ABC là tam giác đều
B. Tam giác ABC là tam giác cân tại C
C. Tam giác ABC là tam giác cân tại A
D. tam giác ABC là tam giác nhọn
Cho tam giác ABC không tù, thỏa mãn điều kiện
cos 2 A + 2 2 cos B + 2 2 cos C = 3
Tính các góc của tam giác ABC
Cho \(cosa=-\dfrac{2}{5}\) và \(\pi< a< \dfrac{3\pi}{2}\)
a) Tính các giá trị lượng giác còn lại của góc a
b) Giá trị biểu thức P = cos2a - cos\(\left(\dfrac{\pi}{3}-a\right)\)
Chứng minh
cos2a - 2cosa. cosb . cos (a + b) + cos2(a+b) = sin2b
Tính sin2a, cos2a, tan2a biết
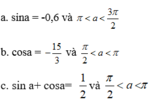
câu20:Cho tana=-2 và pi/2<a<pi.Tính giá trị biểu thức P=cos2a+sin2a
câu21Cho 2tana-cota=1 và -pi/2<a<0.Tính giá trị của biểu thức P=tana+2cota
câu22: Cho sina=-1/7 và pi<a<3pi/2.Tính giá trị của biểu thức P=cos(a+pi/6)
câu23: Cho sina=-1/9; cosb=-2/3 và pi<a<3pi/2; pi/2<b<pi. Tính giá trị của biểu thức P= sin(a+b)
Cho tam giác ABC thỏa mãn hệ thức b + c = 2a. Trong các mệnh đề sau, mệnh đề nào đúng?
A. CosB + Cos C = 2 Cos A B. Sin B + Sin C = 2 Sin A
C. Sin B + Sin C = \(\dfrac{1}{2}SinA\) D. Sin B + Sin C = 2 Sin A
