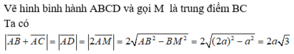Các câu hỏi tương tự
Cho tam giác đều ABC cạnh a, đường cao AH. Hỏi a√3 là độ dài của vectơ nào trong số các vectơ sau đây? A.
A
H
→
B.
A
B
→
-
A
C
→
C.
A
B
→
+
...
Đọc tiếp
Cho tam giác đều ABC cạnh a, đường cao AH. Hỏi a√3 là độ dài của vectơ nào trong số các vectơ sau đây?
A. A H →
B. A B → - A C →
C. A B → + A C →
D. A B → + A C → - A H →
Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ 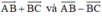
Cho tam giacs ABC có \(^2a=\frac{b^3+c^3-a^3}{b+c-a}\) va a=2bcosC. Chưng minh tam giác ABC đều
Cho tam giác ABC đều cạnh 2a, d là đường thẳng đi qua A và song song vs BC. Khi M di động trên d thì giá trị nhỏ nhất của độ dài vecto MA + 2 * vecto MB là ?
Trong một mặt phẳng oxy cho A (4;6) b (1;4) c (7; 3/2) A. Chứng minh tam giác ABC vuông tại a B. Tính độ dài cạnh ab Có. Tính góc giữa hai vectơ a' b' biết a = (1;2) b (1;3)
Cho a,b,c là độ dài 3 cạnh tam giác.Tìm GTLN của biểu thức P=\(\sqrt{\frac{2a}{2b+2c-a}}+\sqrt{\frac{2b}{2c+2a-b}}+\sqrt{\frac{2c}{2a+2b-c}}\)
Câu 6: Cho tàm giác ABC có A(1; - 1) ;B(2; 0) ;C(3; 5) a) Tìm tọa độ các vecto AB ,AC ,BC b) Tính độ dài các cạnh của tam giác ABC. Từ đó tính chu vi tam giác. c) Tìm tọa độ trung điểm các cạnh và tìm tọa độ trọng tâm của tam giác ABC. d) Tìm tọa độ điểm D để tứ giác ABCD là hnh bình hành e) Tọa độ chân đường cao xuất phát từ A của tam giác. Đ) Tính góc A?
Tam giác ABC có trọng tâm G, độ dài các cạnh BC, CA, AB lần lượt là a, b, c. Khi đó ABC là tam giác đều nếu có điều kiện nào sau đây? A.
a
G
A
→
+
b
G
B
→
+
c
G
C
→
0...
Đọc tiếp
Tam giác ABC có trọng tâm G, độ dài các cạnh BC, CA, AB lần lượt là a, b, c. Khi đó ABC là tam giác đều nếu có điều kiện nào sau đây?
A. a G A → + b G B → + c G C → = 0 →
B. a G A → + b G B → - c G C → = 0 →
C. a G A → - b G B → + c G C → = 0 →
D. - a G A → + b G B → + c G C → = 0 →
tam giác ABC có \(\dfrac{a}{b}=\dfrac{m_b}{m_a}\ne1\). tìm hệ thức đúng
A) \(b^2+c^2=2a^2\) B) \(a^2+c^2=2b^2\)
C) \(a^2+b^2=2c^2\) D) \(2a^2+b^2=c^2\)