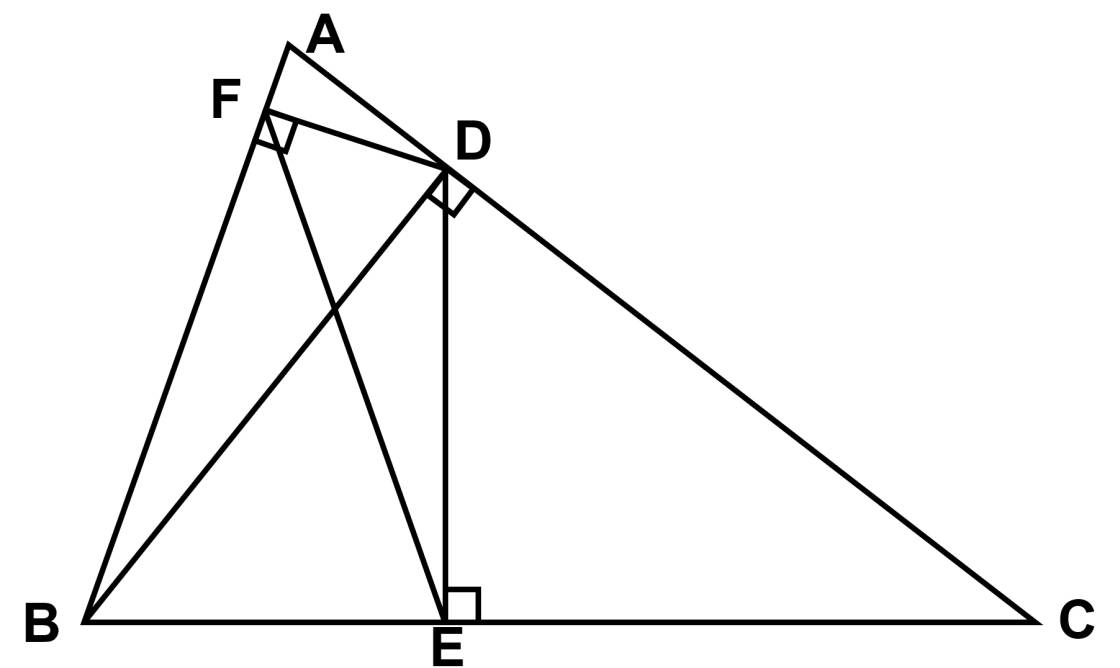
a) xét \(\Delta BDE\) và \(\Delta BCD\), CÓ:
\(\widehat{BDC}=\widehat{DEC}=90^0\)
\(\widehat{DBC}\) chung
\(\Rightarrow\Delta BDE\text{∼}\Delta BDC\left(g.g\right)\)
b) xét \(\Delta BDF\) và \(\Delta BAD\) có:
\(\widehat{BFD}=\widehat{ADB}=90^0\)
\(\widehat{ABD}\) chung
\(\Rightarrow\Delta BDF\text{∼}\Delta BAD\left(g.g\right)\)
\(\Rightarrow\dfrac{BD}{BF}=\dfrac{BA}{BD}\Rightarrow BD\cdot BD=BA\cdot BF\Leftrightarrow BD^2=BA\cdot BF\)
c) xét \(\Delta BEF\) và \(\Delta BAC\), có:
\(\dfrac{BE}{BA}=\dfrac{BF}{BC}\\ \widehat{ABC}chung\\ \Rightarrow\Delta BEF\text{∼}\Delta BCA\left(cgc\right)\\ \Rightarrow\widehat{BFE}=\widehat{ACB}\)