Xét ΔBCK có BC=BK
nên ΔBCK cân tại B
=>\(\widehat{BKC}=\dfrac{180^0-\widehat{KBC}}{2}=\dfrac{\widehat{ABC}}{2}=\widehat{ACB}\)
Xét ΔACB và ΔAKC có
\(\widehat{ACB}=\widehat{AKC}\)
\(\widehat{CAB}\) chung
Do đó: ΔACB~ΔAKC
cho tam giác ABC vuông tại A, BD là phân giác của góc ABC (D thuộc AC). Trên BC lấy điểm K sao cho BK=BA a, Chứng minh tam giác BAD=tam giác BKD. Từ đó suy ra AD=DK b, chứng minh DK vuông góc với BC và góc ABK = góc CDK c, trên tia đối của tia DK lấy điểm E sao cho DE=DC. Chứng minh ba điểm B, A, E thẳng hàng.
Cho tam giác ABC vuông tại B có đường cao BH , AB = 3cm , BC = 4cm . Vẽ phân giác BI của góc ABC
a, Tính độ dài AC, CI
b, Chứng minh tam giác BAC đồng dang tam giác HBC . Tính CH
c,Trên tia đối tia BA lấy điểm D ,Vẽ BK vuông góc CD
Chứng minh BC^2 = CK.CD và tam giác CHK đống dạng tam giác CDA
cho tam giác abc có ab =5 cm ac =12cm , bc=13cm
a, tam giác abc có dạng đặc biệt nào? vì sao?
b,vẽ trung tuyến am của tam giác abc . trên tia đối của tia ma lấy điểm k sao cho mk=ma chứng minh tam giác mkc =tam giác mba .từ đó suy ra kc vuông góc với ac
c, tính độ dài am
2. Cho tam giác ABC vuông tại A (AB<AC), vẽ đường cao AH. Trên đoạn HC lấy điểm M (M không trùng với H,C) từ M vẽ MN vuông góc AC tại N
a) C/M tam giác CMN đồng dạng với tam giác CAH và CA*CN=CH*CM
b) C/m tam giác ADE đồng dạng với tam giác ABC và góc ADE= góc ABC
c) Trên tia đối của tia AC lấy điểm D sao cho AD < AC. Vẽ AE vuông góc BD tại E. Chứng minh góc BEH = góc BCN. Gọi K,F lần lượt là trung điểm BH và BD. I là giao điểm của EK và CF. Chứng minh rằng KC*IE = EF*IC
Cho vuông tại A, đường cao AH.
a) Chứng minh tam giác HBA đồng dạng với tam giác ABC và BA^2=BH.BC
b) Trên tia đối của tia AC lấy điểm D sao cho AD < AC. Vẽ tại AE vuông góc với BD. Chứng minh góc BEH = góc ECD
c) Gọi M là giao điểm của EH và AC. Chứng minh MA^2 = MD.MC
Bài 1 : Cho tam giác ABC có AB=6cm ; AC=10cm ; BC=12cm . Vẽ đường phân giác AD của góc A . Trên tia đối của tia DA lấy điểm I sao cho góc ACI = góc BDA
a) Tính DB , DC
b) Chứng minh tam giác ACI đồng dạng với tam giác CDI
c) Chứng minh AD^2=AB.AC-DB.DC
Cho tam giác ABC, có 2 đường cao AD và CF cắt nhau tại H.
a) Chứng minh tam giác CHD đồng dạng với tam giác CBF
b) Chứng minh góc CDF = góc CHB
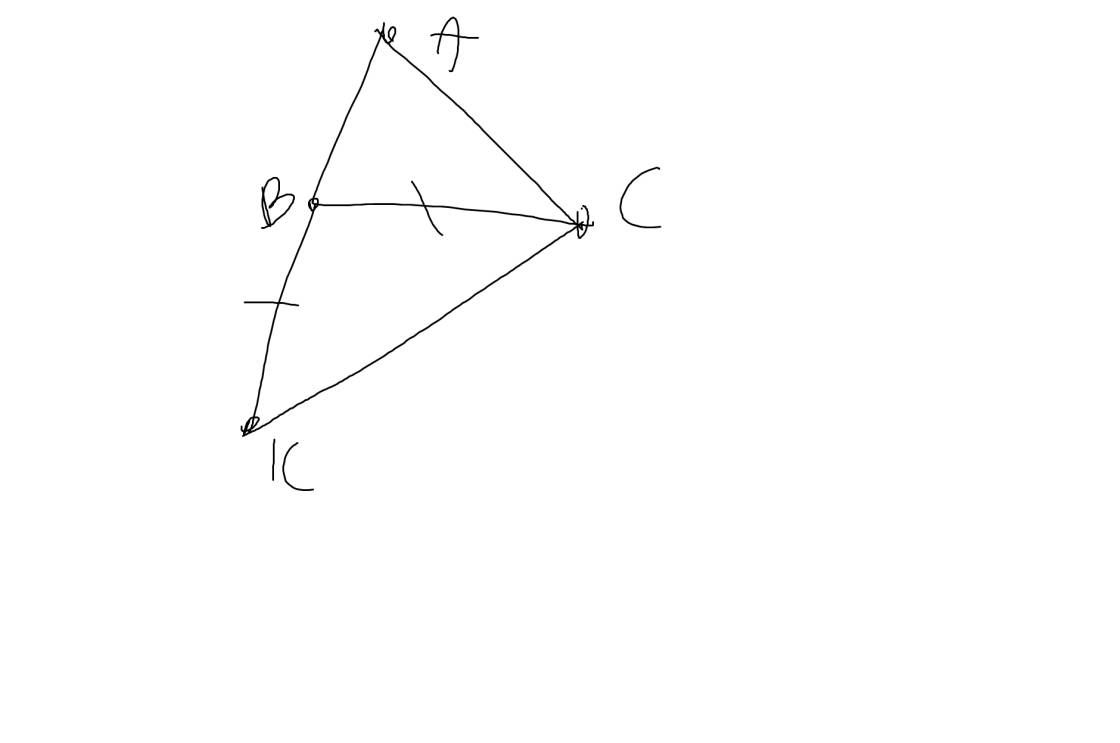
c) Cho goác ABC = 60 độ, ACB = 45 độ. Trên tia đối của tia BA lấy điểm K sao cho góc BCK = 45 độ. Chúng minh tam giác BKD cân.
Cho tam giác ABC vuông tại A có đường cao AH
a) Chứng minh: Tam giác ABC và tam giác HBA đồng dạng rồi suy ra AB^2 = BH . BC
b) CM: Tam giác AHB đồng dạng với tam giác CHA đồng dạng rồi suy ra AH^2 = BH . CH
c) Trên tia đối của tia AC lấy điểm M sao cho AM < AC , vẽ AF vuông góc với BM tại F. Chứng minh góc BFH = góc BAH
cho tam giác ABC vuông tại A(AB<AC) có đường cao AE
a/Chứng minh : tam giác ABC đồng dạng tam giác EAC và AE2 = BE.EC
b/ Trên tia đối tia BA lấy điểm O sao cho BA=BO .Kẻ AD vuông góc OC tại D .Chứng minh : góc EAD = góc BCO
c/ Qua A kẻ đường thẳng vuông góc OE cắt BC tại S .Chứng minh : S là trung điểm EC
cho tam giác ABC, trên tia đối của tia AB lấy D sao cho AD=1/3AB,. Trên tia đối của tia AC lấy E sao cho AE=1/3AC. Chứng minh rằng tam giác ADE đồng dạng tam giác ABC, tìm tỉ số đồng dạng.
Giúp mình với ạ mai mình nộp rồi : ((
