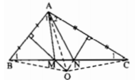
Theo bài 8.3 ta đã có ∠A1 = ∠B1 , ∠A2 = ∠C2 (1)
Ta có O là giao điểm của ba đường trung trực của tam giác ABC nên OA = OB = OC, hay các tam giác OAB, OAC, OBC cân tại O. Suy ra ∠(OAB) = ∠(OBA) , ∠(OAC) = ∠(OCA) , ∠(OBC) = ∠(OCB) . Kết hợp với(1) ∠(OBM) = ∠(OAM) , ∠(OCN) = ∠(OAN) , hay ∠(OAM) = ∠(OBC) = ∠(OCB) = ∠(OAN). Vậy OA là tia phân giác góc MAN.
Cho tam giác ABC có góc A là góc tù. Các đường trung trực của AB ; AC cắt nhau tại O và lần lượt cắt BC tại M, N. Chứng minh rằng AO là phân giác của góc MAN
Cho tam giác ABC có Góc A là góc tù. Các đường trung trực của AB;AC cắt nhau tại O và lần lượt cắt BC tại M,N. CMR AO là tia phân giác của góc MAN
cho tam giác abc có góc a tù. các đường trung trực của Ab và AC cắt nhau tại O và cắt BC theo thứ tự là M và N. chứng minh rằng AO là tia phân giác của góc MAN
Cho tam giác abc có góc a tù. các đường trung trực của Ab và AC cắt nhau tại O và cắt BC theo thứ tự là M và N. chứng minh rằng AO là tia phân giác của góc MAN.
Cho tam giác ABC với góc A là góc tù. Các đường trung trực của AB và AC cắt nhau tại O và cắt BC theo thứ tự tại M và N. Chứng minh rằng: a) ∆AOM = ∆BOM và ∆AON = ∆CON; b) Tia AO là tia phân giác của góc MAN
Cho tam giác ABC có góc A tù. Các đường trung trực của AB và AC cắt nhau tại O và cắt BC theo thứ tự tại M và N. Chứng minh rằng AO tia phân giác của góc MAN.
Cho tam giác ABC không vuông. Các đường trung trực của AB và AC cắt nhau tại O, cắt BC lần lượt tại M và N. Chứng minh rằng AO là tia phân giác của góc MAN
Cho tam giác ABC, có góc A khác 90o. Các đường trung trực của AB và của AC cắt nhau tại O và cắt BC lần lượt theo thứ tự ở M và N. CMR: a/ Góc AOC = 2 góc ABC
b/ AO là tia phân giác của góc MAN
1. cho tam giác ABC vuông tại A. tia phân giác của góc B cắt cạnh AC tại D. kẻ DM vuông góc với BC tại M.
a) Chứng minh: tam giác ABD = tam giác MBD.
b) Gọi giao điểm của DM và AB là E. chứng minh: tam giác BEC cân.
2. cho tam giác ABC có A = 130*. các đường trung trực của AB và AC cắt nhau tại O và cắt BC theo thứ tự M, N.
a) tính số đo gọc MAN.
b) chứng minh AO là phân giác của góc MAN.
