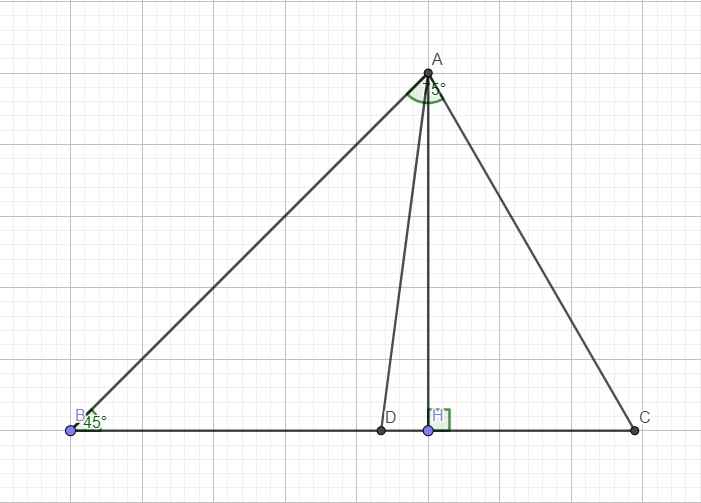
Trong tam giác vuông ABH:
\(tanB=\dfrac{AH}{BH}\Rightarrow AH=BH.tanB=10.tan45^0=10\)
\(cosB=\dfrac{BH}{AB}\Rightarrow AB=\dfrac{BH}{cosB}=\dfrac{10}{cos45^0}=10\sqrt{2}\)
Do tam giác ABH vuông tại H \(\Rightarrow\widehat{BAH}=90^0-\widehat{B}=45^0\)
\(\Rightarrow\widehat{CAH}=\widehat{A}-\widehat{BAH}=75^0-45^0=30^0\)
Trong tam giác vuông ACH:
\(cos\widehat{CAH}=\dfrac{AH}{AC}\Rightarrow AC=\dfrac{AH}{cos\widehat{CAH}}=\dfrac{10}{cos30^0}=\dfrac{20\sqrt{3}}{3}\)
AD là phân giác góc A \(\Rightarrow\widehat{CAD}=\dfrac{1}{2}\widehat{A}=\dfrac{75^0}{2}=37^030'\)
\(\Rightarrow\widehat{DAH}=\widehat{CAD}-\widehat{CAH}=37^030'-30^0=7^030'\)
Trong tam giác vuông ADH:
\(cos\widehat{DAH}=\dfrac{AH}{AD}\Rightarrow AD=\dfrac{AH}{cos\widehat{DAH}}=\dfrac{10}{cos\left(7^030'\right)}\approx10,1\)