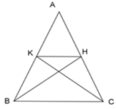
Ta lại có BH và CK là hai đường trung tuyến kẻ từ B và C của tam giác ABC, suy ra H và K lần lượt là trung điểm của AC và AB.
Nên HK là đường trung bình của tam giác ABC nên HK = 1 2 BC = 8 4 = 4cm
Đáp án: B

Ta lại có BH và CK là hai đường trung tuyến kẻ từ B và C của tam giác ABC, suy ra H và K lần lượt là trung điểm của AC và AB.
Nên HK là đường trung bình của tam giác ABC nên HK = 1 2 BC = 8 4 = 4cm
Đáp án: B
Cho DABC có AB = 9cm; AC = 12cm. Trên cạnh AB lấy điểm H và trên cạnh AC lấy điểm K sao cho AH = 6cm; AK = 8cm. a/Cm:HK // BC. b/Cho biết BC = 18cm. Tính HK? c/ Kẻ trung tuyến AM của tam giác ABC ( M thuộc BC). AM cắt HK tại I. Chứng minh rằng I là trung điểm HK.
Cho tam giác abc có ab=9cm ,ac=12cm. Trên cạnh ab lấy điểm H trên cạnh ac lấy điểm K sao cho ah=6cm, ak=8cm
a) cm hk//bc
b)cho biết bc=18cm, Tính HK
c) kẻ trung tuyến am của tam giác abc (M thuộc bc) am cắt hk tại i. Cm i là trung điểm hk
giải với vẽ hình cho mình với
Cho tam giác ABC cân tại A, gọi D và E lần lượt là trung điểm của AB và AC. Gọi H và K lần lượt là chân các đường vuông góc kẻ từ D và E đến BC. Biết BC = 8cm, tính độ dài đoạn thẳng HK.
Cho tam giác ABC vuông tại A biết AB=6cm, AC=8cm. Kẻ đường cao AH (H thuộc BC).
a. Tính BC.
b. Chứng minh tam giác ABC đồng dạng tam giác HBA
c. Chứng minh AB.AC = AH.BC
d. Từ H kẻ HI vuông góc AB (I thuộc AB) và HK vuông góc AC (K thuộc AC). Chứng minh \(\dfrac{AB^3}{AC^3}=\dfrac{BI}{CK}\)
bài 3: tam giác ABC vuông tại A, có AB = 9cm,AC=12cm, dường cao AH:
A)chứng minh tam giác HBA~ tam giác ABC
B) tính dộ dài BC, BH
C) qqua H kẻ HK vuông góc với AB tại K, tính độ dài HK
Cho tam giác cân ABC (AB = AC), vẽ các đường cao BH, CK (h.66).
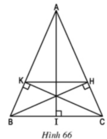
a) Chứng minh BK = CH.
b) Chứng minh KH // BC.
c) Cho biết BC = a, AB = AC = b. Tính độ dài đoạn thẳng HK.
Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm và tam giác HIK vuông tại H có HI = 15cm, IK = 25cm.
a) Tính độ dài BC, HK?
b) Hai tam giác ABC và HIK có đồng dạng với nhau không? Vì sao?
3. Cho tam giác ABC vuông tại B, đường cao BH. Cho AB = 15cm, BC = 20cm. a) Chứng minh: CHB CBA b) Chứng minh: 2 AB AH AC = . c) Tính độ dài AC, BH. d) Kẻ HK AB ⊥ tại K, HI BC ⊥ tại I. Chứng minh BKI BCA e) Kẻ trung tuyến BM của ABC cắt KI tại N. Tính diện tích BKN
a. Cho Tam giác ABC vuông tại A, từ điểm H trên cạnh AC kẻ HK ^ BC tại K. Chứng minh: AB. KC = KH. AC.
b. Cho hình thang ABCD (AB//CD, AB < CD) có AB = 4cm, CD = 16cm, BD = 8cm. Chứng minh: góc DAB và góc DBC.
c. Cho ∆ABC nhọn , hai đường cao AH và BK cắt nhau tại I. Chứng minh: CA.BK = AH.BC.