Đáp án B
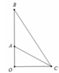
Ta có V = 1 3 π . OC 2 . BO - 1 3 πOC 2 . AO = 1 3 π . OC 2 . AB .
Lại có sin 60 ° = O C A C ⇒ O C = a 3 2 ⇒ V = πa 3 4 .
Đáp án B

Ta có V = 1 3 π . OC 2 . BO - 1 3 πOC 2 . AO = 1 3 π . OC 2 . AB .
Lại có sin 60 ° = O C A C ⇒ O C = a 3 2 ⇒ V = πa 3 4 .
Cho tam giác ABC có A ^ = 120 ° , A B = A C = a . Quay tam giác ABC (bao gồm cả điểm trong tam giác) quanh đường thẳng AB ta được một khối tròn xoay. Thể tích khối tròn xoay đó bằng
A. πa 3 3
B. πa 3 4
C. πa 3 3 2
D. πa 3 3 4
Cho hình phẳng D giới hạn bởi đường cong y = 3 + x − 2 e x x e x + 1 , trục hoành và hai đường thẳng x=0, x=1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V = π a + b ln 1 + 1 e , trong đó a, b là các số hữu tỷ. Mệnh đề nào dưới đây là đúng?
A. a+b=5
B. a-2b=5
C. a+b=3
D. a-2b=7
Cho tam giác ABC cân tại A, góc B A C ^ = 120 ° và AB=4cm. Tính thể tích khối tròn xoay lớn nhất có thể khi ta quay tam giác ABC xung quanh đường thẳng chứa một cạnh của tam giác ABC
A. 16 3 π
B. 16 π 3
C. 16 π 3
D. 16 π
Cho tứ diện ABCD có A D ⊥ A B C , ABC là tam giác vuông tại B. Biết B C = a , A B = a 3 , A D = 3 a . Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
A. 3 3 π a 3 16
B. 8 3 π a 3 3
C. 5 3 π a 3 16
D. 4 3 π a 3 16
Cho tam giác ABC vuông tại A, AB=a, A C = a 3 Quay tam giác đó (cùng với phần trong của nó) quanh đường thẳng BC ta được khối tròn xoay có thể tích V bằng
A. V = πa 3 2
B. V = πa 3 3
C. V = πa 3 24
D. V = 2 πa 3 3
Cho tam giác ABC có AB = 3,BC = 5,CA = 7. Tính thể tích của khối tròn xoay sinh ra là do hình tam giác ABC quay quanh đường thẳng AB:
A. 50 π
B. 75 π 4
C. 275 π 8
D. 125 π 8
Cho tam giác ABC vuông tại A, AB = a, góc ABC bằng 30 o . Quay miền trong tam giác ABC quanh cạnh BC ta được một khối tròn xoay, tính thể tích khối đó?
A. 3 πa 3 2
B. 3 πa 3 18
C. 3 πa 3
D. 3 πa 3 6
Cho tam giác ABC vuông tại A, AB = a, góc ABC bằng 30 ∘ . Quay miền trong tam giác ABC quanh cạnh BC ta được một khối tròn xoay, tính thể tích khối đó?
A. 3 πa 3 18
B. 3 πa 3 6
C. 3 πa 3 2
D. 3 πa 3
Cho ∆ A B C vuông tại A có AB = 3; AC = 4. Quay tam giác quanh AB ta được hình nón tròn xoay có diện tích xung quanh S 1 và quay tam giác quanh AC ta thu được hình nón xoay có diện tích xung quanh S 2 . Tính tỉ số S 1 S 2
A. 4 3
B. 3 4
C. 4 5
D. 3 5