Các câu hỏi tương tự
Cho tam giác ABC có ba góc nhọn, hai đường cao BD và CE của tam giác cắt nhau tại H (D thuộc AC, E thuộc AB)
a) Chứng minh rằng tam giác BHE đồng dạng với tam giác CHD
b) Chứng minh AB.AE = AC.AD
c) Chứng minh góc AED = góc ACB
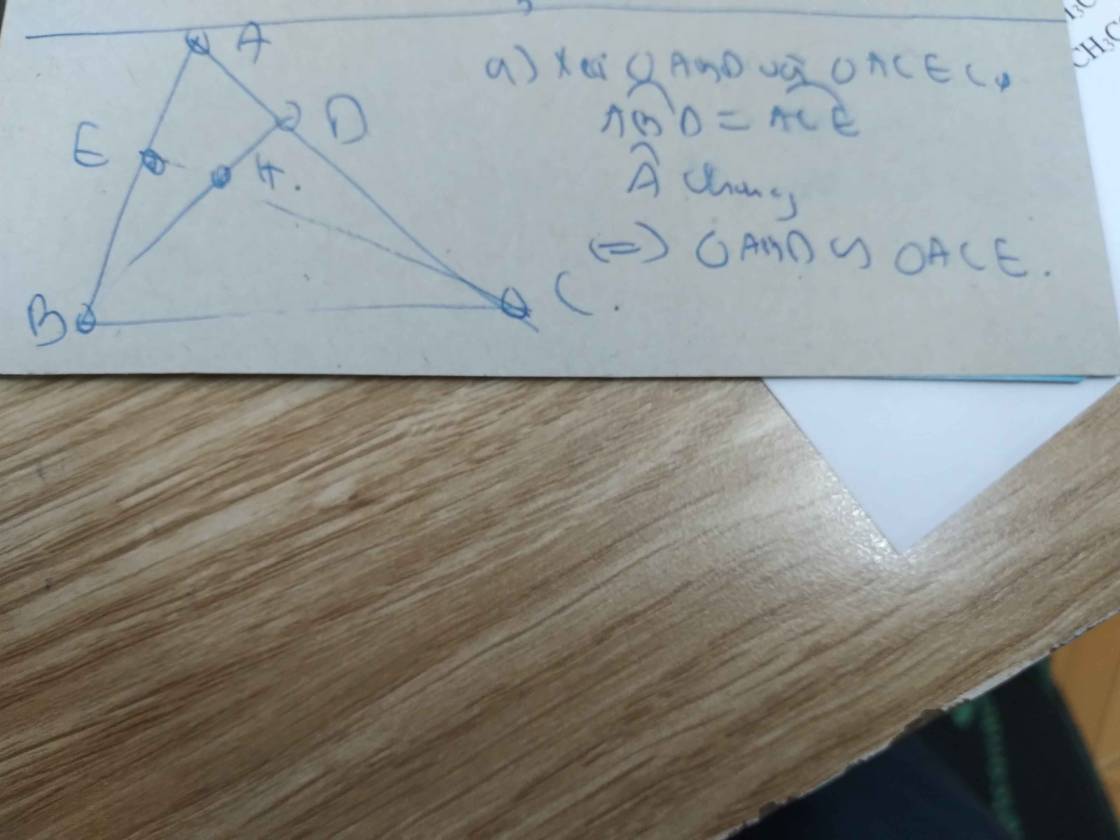
Cho tam giác ABC nhọn(AB<AC), vẽ hai đường cao BD và CE cắt nhau tại H.
a) Chứng minh: Tam giác ABD đồng dạng với tam giác ACE
b)Chứng minh: góc ADE=góc ABC
c) Gọi K là giao điểm của AH và BC. CHứng minh : BD là tia phân giác của góc EDK
d) Chứng minh: BH.BD vuông góc CH.CE=BC.BC
Cho tam giác ABC có ba góc nhọn, hai đường cao BD và CE của tam giác cắt nhau tại H ( D thuộc AC, E thuộc AB).
a) Chứng minh 2 tam giác BHE và CHD đồng dạng
b) Chứng minh AB.AE=AC.AD
c) Chứng minh góc AED = góc ACB
Bài 4: (3 điểm)Cho tam giác ABC có ba góc nhọn (AB AC), hai đường cao BD và CE của tam giác ABC cắt nhau tại H.1) Chứng minh ABD đồng dạng với ACE. Từ đó suy ra AB.AE AC.AD2) Chứng minh ADE đồng dạng với ABC3) Gọi I là giao điểm của DE và CB, M là trung điểm của BC. Chứng minh: ID.IE IM2 – MC2.4) Biết BC 15, tính giá trị biểu thức P BH.BD + CH.CE.
Đọc tiếp
Bài 4: (3 điểm)
Cho tam giác ABC có ba góc nhọn (AB < AC), hai đường cao BD và CE của tam giác ABC cắt nhau tại H.
1) Chứng minh 
ABD đồng dạng với ACE. Từ đó suy ra AB.AE = AC.AD
2) Chứng minh ADE đồng dạng với ABC
3) Gọi I là giao điểm của DE và CB, M là trung điểm của BC. Chứng minh: ID.IE = IM2 – MC2.
4) Biết BC = 15, tính giá trị biểu thức P = BH.BD + CH.CE.
Cho tam giác ABC có 3 góc nhọn, các đường cao BD,CE của tam giác cắt nhau tại H. Chứng minh rằng :
a) Tam giác ABD đồng dạng với tam giác ACE.
b) HE.HC=HD.HB.
c) Kẻ đường vuông góc với AB tại B và đường vuông góc với AC tại C cắt nhau tạ K. Gọi M là trung điểm của BC. Chứng minh: Ba điểm H,M,K thẳng hàng.
Cho tam giác ABC có 3 góc nhọn và AB<AC. Vẽ 2 đường cao BD và CE
a) Chứng minh: Tam giác ABD đồng dạng tam giác ACE. Suy ra AB.AE = AC.AD
b) Chứng minh: Tam giác ABE đồng dạng tam giác ABC
c) Tia DE và CB cắt nhau tại I. Chứng minh: Tam giác IBE đồng dạng tam giác IDC
d) Gọi O là trung điểm của BC. Chứng minh ID.IE = OI2 - OC2
Cho tam giác ABC có 3 góc nhọn và AB < AC . Vẽ hai đường cao BD và CE
a, CM : Tam giác ABD đồng dạng với tam giác ACE . Suy ra AB.AE=AC.AD
b, CM ; tam giác ADE đồng dạng tam giác ABC
c, Tia CE và CB cắt nhau tại I . Chứng minh tam giác IBE đồng dạng với tam giác IDC
d, Gọi O là trung điểm của BC . Chứng minh ID.IE = OI2−OC2
Cho tam giác ABC nhọn, các đường cao BD, CE. Tia phân giác của các góc
A
B
D
^
v
à
A
C
E
^
cắt nhau tại O, và lần lượt cắt AC, AB tại N, M. Tia BN cắt CE tại K, tia CM cắt BD tại H: Chứng minh rằng:a) BN ^ CM;b) Tứ giác MNFIK là hình thoi
Đọc tiếp
Cho tam giác ABC nhọn, các đường cao BD, CE. Tia phân giác của các góc A B D ^ v à A C E ^ cắt nhau tại O, và lần lượt cắt AC, AB tại N, M. Tia BN cắt CE tại K, tia CM cắt BD tại H: Chứng minh rằng:
a) BN ^ CM;
b) Tứ giác MNFIK là hình thoi
Cho tam giác nhọn ABC (AB<AC), các đường cao AD,BE và CF cắt nhau tại H.
a) Chứng minh rằng: Tam giác ABC đồng dạng tam giác ACF và AB.AF = AC.AE
b) Chứng minh rằng: góc AED = góc ACB
c) Gọi M là trung điểm của BC, K là giao điểm của đường thẳng EF và đường thẳng BC. Chứng minh BC2 = 4.MD.MK