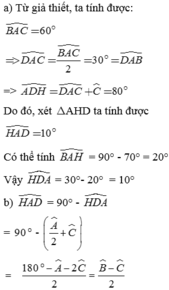Các câu hỏi tương tự
Cho tam giác ABC ( AB>AC ). Trên tia BA lấy điểm D sao cho BD=BC.Nối C với D. Tia phân giác của góc B cắt cạnh AC và CD theo thứ tự ở E và I
.a) Chứng minh tam giác BID = tam giác BIC.
b) Chứng minh ED = EC.
c) Kẻ AH vuông góc với CD tại điểm H , Chứng minh AH song song với BI.
d) Biết số đo góc ABC bằng 70 độ , tính số đo góc BCD và DAH
1. Cho tam giác ABC có AB AC, góc BAC có số đo là 50 độ. Từ B kẻ BH vuông góc với AC tại H, từ C kẻ CK vuông góc với AB tại K.a) Chứng minh: Tam giác ABH tam giác ACK, BH CKb) Gọi O là giao điểm của BH và CK. Tính số đo của góc BOCc) Cho M là trung điểm của BC. chứng minh BC 2MK2. Cho góc xOy bằng 60 độ; Oz là tia phân giác của góc xOy.Trên tia Ox lấy điểm A (A khác O); từ A kẻ đường thẳng vuông góc với Oz cắt Ox tại I và cắt Oy tại B, từ A kẻ đường thẳng song song với Oy cắt Oz tại C.a)Chứn...
Đọc tiếp
1. Cho tam giác ABC có AB = AC, góc BAC có số đo là 50 độ. Từ B kẻ BH vuông góc với AC tại H, từ C kẻ CK vuông góc với AB tại K.
a) Chứng minh: Tam giác ABH = tam giác ACK, BH = CK
b) Gọi O là giao điểm của BH và CK. Tính số đo của góc BOC
c) Cho M là trung điểm của BC. chứng minh BC = 2MK
2. Cho góc xOy bằng 60 độ; Oz là tia phân giác của góc xOy.Trên tia Ox lấy điểm A (A khác O); từ A kẻ đường thẳng vuông góc với Oz cắt Ox tại I và cắt Oy tại B, từ A kẻ đường thẳng song song với Oy cắt Oz tại C.
a)Chứng minh tam giác OAI = tam giác OBI và chứng minh tam giác OAB đều
b)Kẻ AH vuông góc với Oy tại H. Chứng minh AH = CI
c)Từ C kẻ đường thẳng song song với AB cắt Oy tại D. Chứng minh \(AD^2\)= \(3BD^2\)
Giúp mình với!
1. Cho tam giác ABC, góc A 120 độ, đường phân giác AD. Đường phân giác góc ngoài tại C cắt đường thẳng AB ở K. Gọi E là giao điểm của DK và AC. Tính số đo của góc BED.2. Cho tam giác ABC có BC 17cm, CA 15cm, AB 8cm. Ba đường phân giác của tam giác cắt nhau tại O. Tính tổng các khoảng cách từ O đến ba cạnh của tam giác.3. Cho tam giác ABC vuông cân tại A, M là trung điểm của BC. Gọi D là điểm thuộc đoạn MC, H là hình chiếu của B trên AD. Chứng minh HM là tia phân giác của góc BHD.4. Cho tam g...
Đọc tiếp
1. Cho tam giác ABC, góc A = 120 độ, đường phân giác AD. Đường phân giác góc ngoài tại C cắt đường thẳng AB ở K. Gọi E là giao điểm của DK và AC. Tính số đo của góc BED.
2. Cho tam giác ABC có BC = 17cm, CA = 15cm, AB = 8cm. Ba đường phân giác của tam giác cắt nhau tại O. Tính tổng các khoảng cách từ O đến ba cạnh của tam giác.
3. Cho tam giác ABC vuông cân tại A, M là trung điểm của BC. Gọi D là điểm thuộc đoạn MC, H là hình chiếu của B trên AD. Chứng minh HM là tia phân giác của góc BHD.
4. Cho tam giác ABC và điểm I là giao điểm 3 đường phân giác của tam giác. Gọi H là chân đường vuông góc kẻ từ B đến AI. Chứng minh rằng góc IBH = góc ICA.
5. Cho tam giác ABC có góc B = 50 độ, góc C = 20 độ, đường cao AH. Tia phân giác của góc AHC cắt AC tại D. Vẽ tia Ax là tia đối của tia AB. Chứng minh điểm D nằm trên tia phân giác của góc ABC.
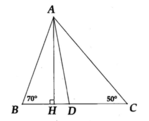
Cho tam giác ABC có B = 70°;C= 30°. Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc với BC ( H∈BC ) .
a ) Tính số đo BAC
b ) Tính số đo ADH
Cho tam giác ABC ( AB < BC ). Trên tia BA lấy điểm D sao cho BD = BC. Nối C với D, đường phân giác của góc B cắt các cạnh AC và CD theo thứ tự ở E và I.
a. Chứng minh hai tam giác HID và HIC bằng nhau.
b. Chứng minh EC = ED.
c. Kẻ AH vuông góc với CD ( H thuộc CD). Chứng minh AC // BI.
d. Biết số đo góc ABC =70•. Tính số đo các góc BCD và DAH.
Bài 1: Cho tam giác ABC có góc A 70*. Tia phân giác của B cắt tia phân giác của C ở I và cắt đường phân giác của góc ngoài tại C ở K. Tính góc BIC và góc BKC.Bài 2: Cho tam giác ABC vuông góc tại A, kẻ đường cao AH. Tia phân giác của góc A cắt BC tại D. Biết góc DAH 15*. Tính các góc của tam giác ABC.Bài 3: Cho tam giác ABC có góc A, B, C là góc nhọn, góc A 50*. Qua B kẻ đoạn thẳng BD vuông góc với AC (D thuộc AC). Qua C kẻ CE vuông góc với AB (E thuộc AB). Gọi H là giao điểm của BD và CE.a)...
Đọc tiếp
Bài 1: Cho tam giác ABC có góc A = 70*. Tia phân giác của B cắt tia phân giác của C ở I và cắt đường phân giác của góc ngoài tại C ở K. Tính góc BIC và góc BKC.
Bài 2: Cho tam giác ABC vuông góc tại A, kẻ đường cao AH. Tia phân giác của góc A cắt BC tại D. Biết góc DAH = 15*. Tính các góc của tam giác ABC.
Bài 3: Cho tam giác ABC có góc A, B, C là góc nhọn, góc A = 50*. Qua B kẻ đoạn thẳng BD vuông góc với AC (D thuộc AC). Qua C kẻ CE vuông góc với AB (E thuộc AB). Gọi H là giao điểm của BD và CE.
a) Tính góc ABD và góc ACE.
b) Tính góc DHE.
Cho tam giác ABC vuông tại A có góc B = 2 lần góc C.
a) Tính số đo góc B và C của tam giác ABC.
b) Kẻ AH vuông góc với BC ( H thuộc BC). Trên tia HC lấy D sao cho H là trung điểm của BD. Chứng minh tam giác ABH = tam giác ADH.
c) Chứng minh: AD = CD
d) Trên tia đối của HA lấy K sao cho HK = H. Chứng minh: KD là đường trung trực của AC.
THanks mina nhìu nhìu !
Cho tam giác ABC cân tại A ( 90 ) A . Hai đường cao BD và CE cắt nhau tại H a) Chứng minh BEC CDB. Từ đó chứng minh BHC cân tại H. b) Từ C kẻ đường thẳng d vuông góc với AC d, cắt đường thẳng AH tại F . Chứng minh CB là tia phân giác của 𝐹𝐶𝐻 ̂; c) Giả sử 𝐵𝐴𝐶 ̂ 60 ; 6 . AB cm Tính khoảng cách từ điểm B đến đường thẳng CF.
Bài 1: (4 điểm) Cho tam giác ABC cân tại A, biết 𝐴 ̂110°.a) Tính số đo 𝐵 ̂, 𝐶 ̂.b) Từ A kẻ AH ⊥ BC (H ∈ BC). Chứng minh AH là tia phân giác của góc A.Bài 2: (6 điểm) Cho tam giác ABC vuông tại B có AB 6 cm, BC 8 cm. Tia phân giác của góc A cắt BC tại E. Từ E kẻ EH ⊥ AC (H ∈ AC).a) Tính độ dài cạnh ACb) Chứng minh ∆ ABE ∆ AHEc) Chứng minh tam giác ABH cân tại A
Đọc tiếp
Bài 1: (4 điểm) Cho tam giác ABC cân tại A, biết 𝐴 ̂=110°.
a) Tính số đo 𝐵 ̂, 𝐶 ̂.
b) Từ A kẻ AH ⊥ BC (H ∈ BC). Chứng minh AH là tia phân giác của góc A.
Bài 2: (6 điểm) Cho tam giác ABC vuông tại B có AB = 6 cm, BC= 8 cm. Tia phân giác của góc A cắt BC tại E. Từ E kẻ EH ⊥ AC (H ∈ AC).
a) Tính độ dài cạnh AC
b) Chứng minh ∆ ABE = ∆ AHE
c) Chứng minh tam giác ABH cân tại A