Đáp án C
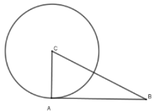
+ Xét tam giác có:
B C 2 = 5 2 = 25 ; A B 2 + A C 2 = 4 2 + 3 2 = 25 ⇒ B C 2 = A B 2 + A C 2
⇒ ΔABC vuông tại A (Định lý Pytago đảo)
⇒ AB ⊥ AC mà A ∈ (C; CA) nên AB là tiếp tuyến của (C; CA)
Đáp án C

+ Xét tam giác có:
B C 2 = 5 2 = 25 ; A B 2 + A C 2 = 4 2 + 3 2 = 25 ⇒ B C 2 = A B 2 + A C 2
⇒ ΔABC vuông tại A (Định lý Pytago đảo)
⇒ AB ⊥ AC mà A ∈ (C; CA) nên AB là tiếp tuyến của (C; CA)
Cho tam giác ABC có AC = 3cm, AB = 4cm, BC = 5cm. Vẽ đường tròn (C; CA). Khẳng định nào sau đây là đúng?
A.Đường thẳng BC cắt đường tròn (C; CA) tại một điểm
B.AB là cát tuyến của đường tròn (C; CA)
C.AB là tiếp tuyến của (C; CA)
D. BC là tiếp tuyến của (C; CA)
Cho tam giác ABC có AB = 6cm;AC=8cm;BC = 10cm; vẽ đường tròn tâm B bán kính BA ;đường tròn tâm C bán kính CA
a, AC là tiếp tuyến của đường tròn tâm B
b, AB là tiếp tuyến của đường tròn tâm C
c, AB cắt đường tròn tâm B tại D, AC cắt được tròn tâm C tại E .M là giao điểm của 2 đường tròn.C.m D,M,E thẳng hàng
- Mình ko làm được ý C, ai giúp mới !!
Cho tam giác ABC có AB=8,AC=6,BC=10.Vẽ đường tròn(C;CA)
a) Chứng minh AB là tiếp tuyến của đường tròn(C)
b) Xác vị trí tương đối của đường thẳng BC với đường tròn(C)
Cho tam giác ABC vuông tại A (AB>AC), có đường cao AH.
1. Cho AB=4cm, AC=3cm. Tính độ dài các đoạn thẳng BC, AH.
2. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong C tại điểm thứ hai D.
a) Chứng minh BD là tiếp tuyến của đường tròn C.
b) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA, BD thứ tự tại E, F. Trên cung nhỏ AD của đường tròn C lấy điểm M bất kỳ, qua M kẻ tiếp tuyến với đường tròn C cắt AB, BD lần lượt tại P, Q. Chứng minh: 2\(\sqrt{PE.QF}\) =EF
Cho đường tròn (O;R) đường kính AB.Lấy điểm C trên cung AB sao cho AC<BC
a)CMR:tam giác ABC vuông
b)Qua A vẽ tiếp tuyến (d) với đường tròn (O),BC cắt (d) tại F.Qua C vẽ tiếp tuyến (d') với đường tròn (O) cắt (d) tại D.CMR:DA=DF
c)Vẽ CH vuông góc với AB ( H thuộc AB),BD cắt CH tại K.CMR:K là trung điểm của CH
d)Tia AK cắt DC tại E.CMR:EB là tiếp tuyến của (O) ,suy ra OE//CA?
Cho đường tròn (O;R), đường kính AB. Vẽ điểm C thuộc đường tròn (O;R) sao cho AC = R. Kẻ OH vuông góc với AC tại H. Qua điểm C vẽ một tiếp tuyến của đường tròn (O;R), tiếp tuyến này cắt đường thẳng OH tại D.
1) Chứng minh AD là tiếp tuyến của đường tròn (O;R).
2) Tính BC theo R và các tỉ số lượng giác của góc ABC
3) Gọi M là điểm thuộc tia đối cua tia CA. Chứng min MC.MA = MO2 – AO2
Cho tam giác ABC vuông tại A có AB = 8cm, AC = 6cm, đường cao AH.
4.1) Tính độ dài đoạn thẳng CH và AH.
4.2) Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường tròn (C) tại điểm thứ hai là D. Chứng minh BD là tiếp tuyến của đường tròn (C).
4.3) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA, BD thứ tự tại E, F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua M kẻ tiếp tuyến với (C) cắt AB, BD lần lượt tại P, Q. Tính chu vi của tam giác BPQ.
4.4). Chứng minh PC² = PE.PQ
Giúp e với ạ mai thi rùi huhu
Cho tam giác ABC nội tiếp trong đường tròn (O). Biết AB=4cm, BC=8,5cm và CA=7,5cm. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F.
a) Chứng minh tam giác ABC vuông và tính độ dài đường cao vẽ từ đỉnh góc vuông của tam giác ABC.
b) Chứng minh rằng EF=2AH.
c) Chứng minh rằng HA là tiếp tuyến của đường tròn (O).
Cho tam giác nhọn ABC (AB<AC) ngoại tiếp đường tròn tâm I. Đường tròn (I) tiếp xúc với các cạnh BC,CA,AB lần lượt tại D,E,F. Đường thẳng EF cắt đường thẳng BC tại M. Đường thằng AD cắt đường tròn (I) tại N(khác D). Chứng minh MN là tiếp tuyến của đường tròn (I).