Áp dụng định lý Ta-lét:
Với EF // CD ta có A F A D = A E A C
Với DE // BC ta có A E A C = A D A B
Suy ra A F A D = A D A B , tức là A F 6 = 6 9
Vậy AF = 6.6 9 = 4 cm
Đáp án: C
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
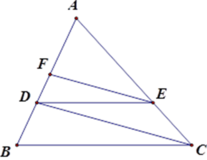
cho tam giác ABC có AB = 9cm; điểm D thuộc cạnh AB sao cho AD = 6cm. Kẻ DE//BC (E thuộc AC) , Kẻ EF//CD ( F thuộc AB ). Độ dài cạnh AF là ... cm :))
Cho tam giác ABC có AB = 9cm; điểm D thuộc cạnh AB sao cho AD = 6cm.
Kẻ DE // BC (E thuộc AC), kẻ EF // AD (F thuộc AB).
Độ dài cạnh AF là ............... cm.
Cho tam giác ABC. Lấy điểm D thuộc cạnh AB sao cho: AD= 4,5 cm, BD= 5,5 cm. Qua D kẻ đường thẳng song song với BC cắt AC tại E. Qua E kẻ đường thẳng song song với AB cắt BC tại F. Biết BF = 6 cm. Tính BC
Cho tam giác abc cân tại a ab=ac=20cm bc=24cm trên cạnh ab lấy điểm e sao cho ae=af=16cm trên cạnh ac lấy điểm f sao cho ae=à=16cm
a,CM ef song song với bc
b,tính độ dài ei
c, kẻ đường cao ah,bk cắt nhau tại i CM tam giác hbi đồng dạng với tam giác hac
d, tính độ dài ih,bi
Các bạn không cần vẽ hình đâu chỉ cần giải ra thôi1) Cho hình bình hành ABCD E là điểm trên AB. DE kéo dài cắt đường thẳng BC tại FChứng minh tam giác ADE đồng dạng với tam giác BFE2) Cho tam giác ABC vuông góc tại A với AC bằng 3 cm BC bằng 5cm Vẽ đường cao AKChứng minh rằng tam giác ABC đồng dạng với tam giác KBA và AB2 BK.BC3) Cho tam giác ABC có AB 15cm AC 20cm BC 25 cm. Trên cạnh AB lấy điểm E sao cho AE 18cm trên cạnh AC lấy F sao cho AF 6 cmSo sánh AE/AC;AF/AB4) Cho tam giác ABC vuôn...
Đọc tiếp
Các bạn không cần vẽ hình đâu chỉ cần giải ra thôi
1) Cho hình bình hành ABCD E là điểm trên AB. DE kéo dài cắt đường thẳng BC tại F
Chứng minh tam giác ADE đồng dạng với tam giác BFE
2) Cho tam giác ABC vuông góc tại A với AC bằng 3 cm BC bằng 5cm Vẽ đường cao AK
Chứng minh rằng tam giác ABC đồng dạng với tam giác KBA và AB2 = BK.BC
3) Cho tam giác ABC có AB = 15cm AC = 20cm BC = 25 cm. Trên cạnh AB lấy điểm E sao cho AE 18cm trên cạnh AC lấy F sao cho AF = 6 cm
So sánh AE/AC;AF/AB
4) Cho tam giác ABC vuông tại A đường cao AH cắt phân giác BD tại I
Chứng minh rằng a,IA.BH = IH.BA
b,Tam giác ABC đồng dạng với tam giác HBA
5) cho tam giác AOB có AB bằng 18 cm OA = 12 cm OB = 9cm. Trên tia đối của tia OB lấy điểm D sao cho OD bằng 3 cm. Qua D kẻ đường thẳng song song với AB cắt AO ở C. Gọi F là giao điểm của AD và BC
Tính độ dài OC;CD
6) Cho tam giác nhọn ABC có AB bằng 12 cm AC bằng 15 cm. Trên các cạnh AB và AC lấy các điểm D và E sao cho AD = 4 cm,AE = 5cm
Chứng minh rằng DE // BC, Từ đó suy ra tam giác ADE đồng dạng với tam giác ABC?
7) Cho tam giác ABC vuông tại A D nằm giữa A và C. Kẻ đường thẳng D vuông góc với BC tại E và cắt AB tại F
Chứng minh tam giác ADF đồng dạng với tam giác EDC
Bài 5. Cho tam giác ABC vuông tại A. Từ một điểm D tùy ý trên cạnh BC, kẻ DE song song với AC (E thuộc AB), DF song song với AB (F thuộc AC). a) Tứ giác AEDF là hình gì? Vì sao? b) Tìm vị trí của điểm D trên cạnh BC để đoạn thẳng EF có độ dài nhỏ nhất.
câu 1:cho tam giác abc, điểm d thuộc cạnh bc. qua d kẻ đường thẳng song song với ac, ab , chúng cắt ab , ac theo thứ tự ở e, f . cm
\(\frac{ae}{ab}\)+\(\frac{af}{ac}\)=1
câu 2 : Cho tam giác abc(ab<ac), đường phân giác ad. Qua trung điểm m của bc , kẻ đường thẳng song song với ad , cắt ac và ab theo thứ tự ở e và k .cm
a)ae=ak
b)bk=ce
1) Cho tam giác ABC, điểm I thuộc đường trung tuyến AM. Gọi E là giao điểm của BI và AC, F là giao điểm của CI và AB. G là trung điểm BF, H là trung điểm CE. CMR: EF//BC 2) Cho hình thang ABCD (AB//CD) có AB12, CD15. Gọi M là trung điểm AB, E là giao điểm CM và AD, F là giao điểm của DM và BC. Tính độ dài EF 3) Cho hình bình hành ABCD, E thuộc AD, F thuộc AB, I thuộc AC. Gọi M là giao điểm FI và CD, K là giao điểm EI và BC. CMR: MK//EF4) Cho tam giác ABC, AB10, AC15, 1 đường thẳng đi qua điểm...
Đọc tiếp
1) Cho tam giác ABC, điểm I thuộc đường trung tuyến AM. Gọi E là giao điểm của BI và AC, F là giao điểm của CI và AB. G là trung điểm BF, H là trung điểm CE. CMR: EF//BC
2) Cho hình thang ABCD (AB//CD) có AB=12, CD=15. Gọi M là trung điểm AB, E là giao điểm CM và AD, F là giao điểm của DM và BC. Tính độ dài EF
3) Cho hình bình hành ABCD, E thuộc AD, F thuộc AB, I thuộc AC. Gọi M là giao điểm FI và CD, K là giao điểm EI và BC. CMR: MK//EF
4) Cho tam giác ABC, AB=10, AC=15, 1 đường thẳng đi qua điểm M thuộc cạnh AB và song song với BC cắt AC ở N sao cho AN=BM. Tính độ dài AM sao cho AM=BN
5) Cho tam giác ABC có AB<AC, đường phân giác AD, lấy I thuộc BC sao cho BI=2 IC. Qua I kẻ đường thẳng song song với AD cắt AC và AB theo thứ tự ở E và K. CM BK= 2 CE
Cho tam giác ABC vuông tại A có AB = 6 cm, AC= 10 cm. Tia phân giác góc A cắt BC tại D. Qua D kẻ đường thẳng song song với AB cắt AC tại E. Tính BC, BD,CD, DE,CE,AE