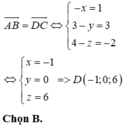Các câu hỏi tương tự
Cho tam giác ABC có
A
1
;
-
2
;
0
,
B
2
;
1
;
-
2
,
C
0
;
3
;
4
. Tìm tọa độ điểm D để tứ gi...
Đọc tiếp
Cho tam giác ABC có A 1 ; - 2 ; 0 , B 2 ; 1 ; - 2 , C 0 ; 3 ; 4 . Tìm tọa độ điểm D để tứ giác ABCD là hình bình hành
A. - 1 ; 0 ; 6
B. 1 ; 6 ; 2
C. 1 ; 6 ; - 2
D. 1 ; 0 ; - 6
Cho hình bình hành ABCD có DT = 4 biết A(1;0) và B(2;0). Giao điểm I của 2 đg chéo AC và BD nằm trên đg thẳng y=x. Tìm tọa độ C&D.
Cho ba điểm A(2;1); B(2;-1); C(-2;-3) Tìm tọa độ điểm D sao cho ABCD là hình bình hành
A. D(2;-1)
B. D(-1;-2)
C. D(-2;-1)
D. D(-2;1)
Trong mặt phẳng Oxy cho tam giác ABC có A(2;1), B(-1;2), C(3;0). Tứ giác ABCE là hình bình hành khi tọa độ E là cặp số nào sau đây?
A. (6;-1).
B. (0;1).
C. (1;6).
D. (6;1).
Trong không gian tọa độ với hệ tọa độ Oxyz, cho ba điểm A(1;2;-1), B(2;-1;3) và C(-3;5;1). Gọi điểm D(a;b;c) thỏa mãn tứ giác ABCD là hình bình hành. Tính tổng T = a + b + c.
A. T = 1.
B. T = 5.
C. T = 3.
D. T = -1.
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có tọa độ các điểm A(1;1;1), B(2;0;2), C(-1;-1;0), D(0;3;4). Trên các cạnh AB, AC, ADlần lượt lấy các điểm B’,C’,D’ sao cho
A
B
A
B
+
A
C
A
C
+
A
D...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có tọa độ các điểm A(1;1;1), B(2;0;2), C(-1;-1;0), D(0;3;4). Trên các cạnh AB, AC, ADlần lượt lấy các điểm B’,C’,D’ sao cho A B A B ' + A C A C ' + A D A D ' = 4 và tứ diện AB’C’D’ có thể tích nhỏ nhất. Phương trình mặt phẳng (B’C’D’) là
A. 16x-40y-44z-39=0.
B. 16x-40y-44z+39=0.
C. 16x+40y+44z-39=0.
D. 16x+40y-44z+39=0.
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(0;1;1), B(1;-2;0), C(-2;1;-1). Diện tích tam giác ABC là
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(0;1;1), B(1;-2;0), C(-2;1;-1). Diện tích tam giác ABC là
![]()
![]()
![]()
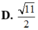
Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD có diện tích bằng 16. Biết tam giác ABC cân tại A, cạnh BC4 và
K
(
21
5
;
18
5
)
là hình chiếu của điểm B xuống AC. Tìm tọa độ điểm D biết rằng điểm B thuộc đường thẳng
△
:
x
+
y
-
3
0
đồng thời hoành độ các điểm B, C đều là các số nguyên A....
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD có diện tích bằng 16. Biết tam giác ABC cân tại A, cạnh BC=4 và K ( 21 5 ; 18 5 ) là hình chiếu của điểm B xuống AC. Tìm tọa độ điểm D biết rằng điểm B thuộc đường thẳng △ : x + y - 3 = 0 đồng thời hoành độ các điểm B, C đều là các số nguyên
A. D(5;2)
B. D(7;6)
C. (-7;-6)
D. D(-5;-2)
Trong không gian với hệ trục tọa độ Oxyz, cho A(0;-1;1), B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là: A.
D
−
1
;
1
;
2
3
B.
D
1
;
3...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho A(0;-1;1), B(-2;1;-1), C(-1;3;2). Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là:
A. D − 1 ; 1 ; 2 3
B. D 1 ; 3 ; 4
C. D 1 ; 1 ; 4
D. D − 1 ; − 3 ; − 2