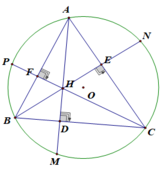
d) Tam giác ADB vuông tại D có: ∠(A1) + ∠(ABC) = 90o (1)
Tam giác BCF vuông tại F có: ∠(C1) + ∠(ABC) = 90o (2)
Từ (1)và (2) ⇒ ∠(A1) = ∠(C1)
Mặt khác, ta có: ∠( A 1 ) = ∠( C 2 ) ( 2 góc nội tiếp cùng chắn cung BM)
⇒ ∠( C 1 ) = ∠( C 2 )
⇒ CD là tia phân giác của góc HCM
Xét tam giác HCM có: CD vừa là tia phân giác vừa là đường cao (CD⊥HD)
⇒ Δ HCM cân tại C
⇒ CD cũng là trung tuyến của của HM hay H và M đối xứng với nhau qua D.










