Chọn đáp án B.
Ta có: BD và CE là đường cao của tam giác ABC nên 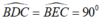
Trên cùng 1 nửa mặt phẳng bờ BC, hai điểm D và E cùng nhìn đoạn thẳng BC dưới 1 góc vuông nên 4 điểm B, C, D, E cùng thuộc 1 đường tròn hay tứ giác BCDE là tứ giác nội tiếp .
Chọn đáp án B.
Ta có: BD và CE là đường cao của tam giác ABC nên 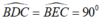
Trên cùng 1 nửa mặt phẳng bờ BC, hai điểm D và E cùng nhìn đoạn thẳng BC dưới 1 góc vuông nên 4 điểm B, C, D, E cùng thuộc 1 đường tròn hay tứ giác BCDE là tứ giác nội tiếp .
1.Cho tam giác ABC nhọn. Kẻ các đường cao BD, CE cắt nhau tại H. Chứng mình rằng: a,AEHD là tứ giác nội tiếp b,BEDC là tứ giác nội tiếp. Tìm tâm đường tròn ngoại tiếp c, Góc EBD=ECD d,AH vuông góc với BC
2.Cho tam giác ABC có 3 góc nhọn. Các đường cao BM và CN cát nhau tại I. Chứng minh rằng: a,AMIN là một tứ giác nội tiếp b, Góc NAI=NMI c,AI cắt BC tại H. Chứng minh HA là tia phân giác của góc NHM
cho tam giác ABC nhọn (AB<AC) nội tiếp đường tròn tâm (O) . Đường cao BD và đường cao CE cắt nhau tại H , BD cắt CE tại F, AF cắt đường tròn (O) tại K.
a, Cm : tứ giác BCDE nội tiếp, xác định tâm đường tròn.
b, cm : FA .FK = FE.FD;
c. CM : FH vuông góc với AM
Cho tam giác ABC (AB > AC) nội tiếp đường tròn tâm O. Các đường cao BD và CE cắt nhau tại H (D thuộc AC, E thuộc AB). Gọi M, N lần lượt là trung điểm của các cạnh AB và AC. a) Chứng minh các tứ giác BCDE, AMON nội tiếp. b) Chứng minh: AE.AM = AD.AN c) Gọi K là giao điểm của ED và MN, F là giao điểm của AO và MN, I là giao điểm của ED và AH. Chứng minh: F là trực tâm của tam giác KAI.
ch tam giác nhọn ABC nội tiếp trong đường tròn tâm O đường cao BD và CE cắt nhau tại H
a) cm các tứ giác ADHE và BCDE nội tiếp
b0 tia BD và CE lần lượt cắt đường tròn (O)tại M và N CM DE//MN
Cho tam giác ABC nhọn nội tiếp trong đường tròn tâm O. Các đường cao BD và CE của tam giác cắt nhau tại H. Chứng minh rằng rằng:
A) Tứ giác BCDE nội tiếp đường tròn, từ đó suy ra góc BCD = góc AED
B) Kẻ đường kính AK, chứng minh AB.BC = AK.BD
C) Từ điểm O kẻ OM vuông góc với BC Chứng minh H, K, M thẳng hàng
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Hai đường cao BD, CE của tam giác ABC cắt nhau tại H. a) Chứng minh tứ giác BFEC nội tiếp được một đường tròn. b) Kẻ đường kính AD của đường tròn (O). Tứ giác BFCD là hình gì? Vì sao? c) Gọi M là trung điểm của BC. Chứng minh AH = 2OM. d) Chứng minh OA | EF
cho tam giác ABC nhọn , AB<AC nội tiếp đường tròn (O). Các đường cao BD và CE của tam giác ABC cắt nhau tại H. Gọi K là giao điểm của DE và CB.
a)CMR: Tứ giác BCDE nội tiếp
b) C/m : KB.KC=KE.KD
c) Gọi M là trung điểm của BC , AK cắt đường tròn (O) tại điểm thứ 2 N . C/m : 3 điểm M,H,N thẳng hàng
Cho tam giác ABC nhọn nội tiếp (O). Các đường cao BD và CE của tam giác cắt nhau tại H.
a) CM: tứ giác BCDE nội tiếp đường tròn tâm O.
b) Kẻ đường kình AK. CM: AB.BC = AK.BD.
c) CM: góc BCD = góc AED
d) Từ O kẻ OM vuông góc BC. CM: H, M, K thẳng hàng.
Cho tam giác ABC nhọn ( AB < AC) nội tiếp đường tròn (O;R). Vẽ đường cao BD và CE cắt tại H{ với De AC; E = AB). BD và CE lần
lượt cắt đường tròn tại M và N.
a) Chứng minh tứ giác BCDE nội tiếp đường tròn. b) Biết overline ACN = 30 deg . Tính số đo các cung nhỏ AN, MN
c) Chứng minh :OA 1 MN.
d) Gọi giao điểm của AH và BC là K. Chứng minh 2R.AK = AB.AC