Các câu hỏi tương tự
Cho tam giác ABC cân tại A.Trên 2 cạnh AB và AC lần lượt lấy 2 điểm E và F sao cho AE + AF = AB.Gọi M là trung điểm của EF.Chứng minh rằng M luôn nằm trên 1 đường thẳng cố định
Cho tam giác ABC vuông tại A có AB<AC, đường cao AH và trung tuyến AE. Gọi D, F lần lượt là hình chiếu của E trên AB, AC. Lấy M sao cho F là trung điểm của EM và N sao cho F là trung điểm của BN. Chứng minh A, N, M thẳng hàng
Cho tam giác ABC nhọn (ABAC), kẻ đường cao AH. Gọi M,N,D lần lượt là trung điểm các cạnh BC,BA,AC.a) Cm: ND là trung trực của đoạn thẳng AH và thứ giác MDNH là hình thang cân b) Giả sử HD vuông góc MN. Cm AHND+MHc) Trong trường hợp tím giác MDNH có góc MD90 và MHMDDN:2. Lấy điểm E bất kì thuộc cạnh MH (E khác M,H), kẻ tia Ex vuông góc với DE và tia này cắt cạnh NH tạo F. Cm tam giác DEF vuông cân
Đọc tiếp
Cho tam giác ABC nhọn (AB<AC), kẻ đường cao AH. Gọi M,N,D lần lượt là trung điểm các cạnh BC,BA,AC.
a) Cm: ND là trung trực của đoạn thẳng AH và thứ giác MDNH là hình thang cân
b) Giả sử HD vuông góc MN. Cm AH=ND+MH
c) Trong trường hợp tím giác MDNH có góc M=D=90 và MH=MD=DN:2. Lấy điểm E bất kì thuộc cạnh MH (E khác M,H), kẻ tia Ex vuông góc với DE và tia này cắt cạnh NH tạo F. Cm tam giác DEF vuông cân
cho tam giác abc vuông tại a (ab<ac).Vẽ đường cao ah, gọi m,n lần lượt là trung điểm ah, bh.
A) chứng minh tứ giác abnm là hình thang
B) gọi d là trung diểm của cạnh bc, từ d kẻ đg thẳng song song với ac, ab và lần lượt cắt ab tại e, cắt ac tại f. Chứng minh tứ giác aedf là hình chữ nhật
1, Cho tam giác ABC có I là trung điểm của cạnh BC. Qua I kẻ đường thẳng d cắt AB,AC lần lượt tại M và N . Kẻ dường thẳng d' cắt AC,AB lần lượt tại E,F . CMR : IE=IF
2, cho hình thoi ABCD có góc B bằng 60 độ . Một đường thẳng đi qua D cắt đường kéo dài các cạnh AB,BC lần lượt tại E và F. Gọi M là giao điểm của AF, CE . Chứng minh rằng : AD^2 = AM.AF
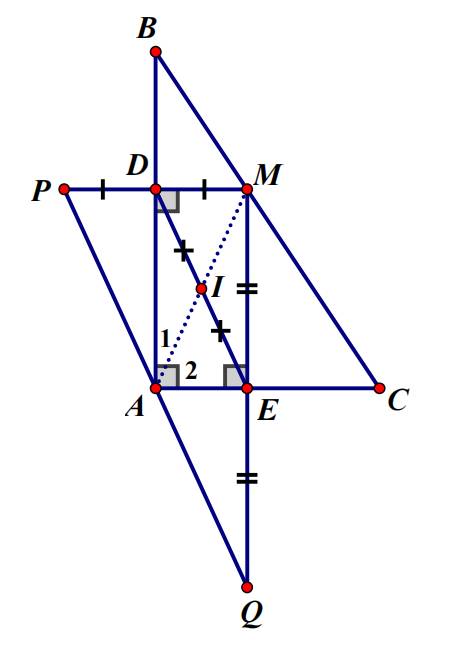
Bài 2: Cho △ABC vuông tại A. Lấy điểm M thuộc cạnh BC. Kẻ MD và ME lần lượt vuông góc với AB và AC ( D thuộc AB, E thuộc AC ). Lấy I là trung điểm của DE. a) Tứ giác ADME là hình gì? Vì sao? b) Chứng minh ba điểm A, I, M thẳng hàng. c) Trên tia đối của tia DM lấy điểm P, trên tia đối của tia EM lấy điểm Q sao cho, DPDM, EQEM Chứng minh A, P, Q thẳng hàng và A là trung điểm PQ
Đọc tiếp
Bài 2: Cho △ABC vuông tại A. Lấy điểm M thuộc cạnh BC. Kẻ MD và ME lần lượt vuông góc với AB và AC ( D thuộc AB, E thuộc AC ). Lấy I là trung điểm của DE.
a) Tứ giác ADME là hình gì? Vì sao?
b) Chứng minh ba điểm A, I, M thẳng hàng.
c) Trên tia đối của tia DM lấy điểm P, trên tia đối của tia EM lấy điểm Q sao cho, DP=DM, EQ=EM
Chứng minh A, P, Q thẳng hàng và A là trung điểm PQ
Cho tam giác ABC nhọn ( AB < AC). Gọi E, F, I lần lượt là trung điểm của AB, AC, BC. Kẻ AH là đường cao của tam giác ABC.
a) Chứng minh EFIH là hình thang cân.
b) Biết AH cắt EF tại K. Kẻ ED, FM cùng vuong góc với BC tại D và M. Chứng minh ME, DF, KI đồng quy tại O.
c) Gọi AD cắt EH tại R. Chứng minh R, O, C thẳng hàng.
Cho tam giác ABC vuông tại A. AB 7,5 cm; BC 12,5 cm. a) Tính diện tích tam giác ABC. b) Lấy điểm M trên cạnh AB sao cho AM : MB 1 : 2. Từ M kẻ đường thẳng song song với BC cắt trung tuyến AF tại E và cắt cạnh AC tại N. Chứng minh E là trung điểm của MN. c) Gọi G, H lần lượt là trung điểm của MC, BN. Chứng minh EGFH là hình chữ nhật và tính diện tích của nó.
Đọc tiếp
Cho tam giác ABC vuông tại A. AB = 7,5 cm; BC = 12,5 cm.
a) Tính diện tích tam giác ABC.
b) Lấy điểm M trên cạnh AB sao cho AM : MB = 1 : 2. Từ M kẻ đường thẳng song song với BC cắt trung tuyến AF tại E và cắt cạnh AC tại N. Chứng minh E là trung điểm của MN.
c) Gọi G, H lần lượt là trung điểm của MC, BN. Chứng minh EGFH là hình chữ nhật và tính diện tích của nó.
Cho tam giác ABC vuông tại A (AB<AC) đường cao AH. Trên HC lấy điểm M sao cho MH=AH. Từ M kẻ đường thẳng song song với AH cắt đường thẳng kẻ từ A song song với BC tại E.
a) tứ giác AHME là hình gì ?
b) Cho AC cắt ME tại F. CM: AB=AF
c) Gọi N là trung điểm của BF. CM:H,N,F thẳng hàng
d) Tìm đk của tam giác ABC để SAHME=SABC











