Question

cho tam giác ABC cân tại A,các đường cao BD và CE cắt nhau tại H

a) chứng minh:AD=AE

b) chứng minh:AH đi qua trung điểm của BC

c) chứng minh: DE//BC

Answer 1

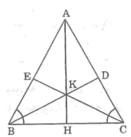
(Bạn tự vẽ hình nhé)

a/ Xét tam giác ABC có 2 đường cao BD;CE cắt nhau tại H => H là trực tâm tam giác ABC => AH là đường cao thứ 3 (=> AH vuông góc BC)

Vì tam giác ABC cân tại A => AH vừa là đường cao vừa là phân giác => góc EAH = góc DAH

Xét tam giác AEH và tam giác AHD có:

   góc EAH = góc DAH (cmt)

  AH: chung

  góc AEH = góc ADH = 90 độ (gt)

=> tam giác AEH = tam giác ADH (g.c.g)

=> AD = AE (2 cạnh t.ứng)

b/ Vì tam giác ABC cân tại A nên AH cũng là đường trung tuyến

=> AH đi qua trung điểm BC

c/ Ta có: AE = AD (cmt)

              EH = DH (vì tam giác AEH = tam giác ADH)

=> AH là đường trung trực của ED 

=> AH vuông góc ED (tới đây thôi được r` dù còn 1 tính chất đường trung trực nữa. Nhưng nếu suy ra phải thêm điểm cơ)

Mà: AH vuông góc BC (gt)

=> DE // BC