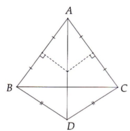
Từ giả thiết, ta có: AB = AC, DB = DC.
=> AD là đường trung trực của BC.
Xét tam giác ABC, theo tính chất ba đường trung trực trong tam giác ta có các đường trung trực của AB và AC đồng quy với đường thẳng AD.

Từ giả thiết, ta có: AB = AC, DB = DC.
=> AD là đường trung trực của BC.
Xét tam giác ABC, theo tính chất ba đường trung trực trong tam giác ta có các đường trung trực của AB và AC đồng quy với đường thẳng AD.
Cho tam giác ABC vuông tại A. Trên nửa mặt phẳng bờ BC không chứa A dựng tam giác BCD vuông cân tại D. Hạ D I ⊥ A B , D H ⊥ A C .
Chứng minh AD là tia phân giác của A ^
CHo tam giác ABC vuông tại góc A . Trên nửa mặt phẳng bờ BC không chứa điểm A dựng tam giác BCD vuông cân tại D . Chứng minh AD là tia phân giác của góc BAC
cho tam giác ABC vuông tại A. Trên nửa mặt phẳng bờ BC ko chứa điểm A dựng tam giác BCD vuông cân tại D. Chứng minh AD là tia phân giác của góc A
cho tam giác ABC vuông tại A. Trên nửa mặt phẳng bờ BC ko chứa điểm A dựng tam giác BCD vuông cân tại D. Chứng minh AD là tia phân giác của góc A
Cho tam giác ABC vuông tại A, AB > AC. Đường cao AH. D là điểm nằm trên nửa mặt phẳng bờ BC không chứa A và tam giác DBC cân tại D. Đường trung trực của AB cắt BC tại E. Chứng minh DE vuông góc BC
cho tam giác ABC vuông tại A có AB<AC. trên một nửa mặt phẳng bờ BC ko chứa A, vẽ tam giác BCD vuông cân tại D.
a. chứng minh rằng ABD+ACD=180độ.
b. qua D kẻ đường thẳng vuông góc với AD cắt đường thẳng AC tại E. chứng minh rằng DA=DE.
c. chứng minh rằng AD là tia phân giác của BAC.
d. gọi M là trung điểm của BC. chứng minh rằng MA=MD.
1, Cho tam giác ABC nhọn, trung tuyến AI. Trên nửa mặt phẳng bờ AC không chứa điểm B lấy điểm M sao cho tam giác ABM vuông cân tại A. Trên nửa mặt phẳng bờ Ab không chứa điểm C lấy điểm N sao cho tam giác ACN vuông cân tại A. Chứng minh rằng đường thẳng AI vuông góc với đường thẳng BC
2, Cho tam giác ABC cân tại A, M thuộc cạnh BC sao cho MB < MC. Lấy O thuộc đoạn thẳng AM. Chứng minh rằng \(\widehat{AOB}>\widehat{AOC}\)
Cho tam giác ABC cân tại A, kẻ AD là đường trung tuyến của tam giác. Kéo dài tia AD, trên tia này lấy điểm MC, MA nằm khác phía so với nửa mặt phẳng bờ chứa tia BC. Chứng minh: AM là đường trung trực của đoạn thẳng BC
Cho tam giác ABC nhọn. Trên nửa mặt phẳng bờ AB không chứa C dựng đoạn thẳng AD vuông góc với AB và AD = AB, Trên nửa mặt phẳng bờ AC không chứa điểm B dựng đoạn thẳng AE vuong góc với AC và AC = AE, Vẽ AH vuông góc với BC, Đường thẳng HA cắt DE ở K. Chứng minh: K là trung điểm của DE.