Các câu hỏi tương tự
Cho tam giác ABC cân tại A. Gọi M là trung điểm của BC Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho góc DME bằng góc B. Chứng minh rằng
a, BD.CE=\(\frac{1}{4}BC^2\)
b, DM là phân giác của góc BDE
c, Chu vi tam giác ADE không đổi khi D, E chuyển động trên AB,AC
Cho tam giác ABC cân tại A, M là trung điểm của BC. lấy các điểm D và E theo thứ tự thuộc các cạnh AB, AC sao cho góc DME = góc B
a. Chứng minh tam giác BDM đồng dạng với tam giác CME
b. BD . CE không đổi
c. DM là phân giác của góc BDE.
Cho tam giác ABC cân tại A, M là trung điểm của BC. lấy các điểm D và E theo thứ tự thuộc các cạnh AB, AC sao cho góc DME = góc B
a. Chứng minh tam giác BDM đồng dạng với tam giác CME
b. BD . CE không đổi
c. DM là phân giác của góc BDE.
Làm giúp mình câu c thật chi tiết với nhé còn câu a và b mình làm được rồi. Cảm ơn
Cho tam giác ABC cân tại A , M là trung điểm của BC trên cạnh AB lấy D, AC lấy E sao cho DM là tia pg của góc BDE
Cmr:
a, EM là tia pg của góc CED
b, tam giác BDM đồng dạng tam giác CME
c, BD.CE=a^2 (a=BM)
Cho tam giác đều ABC , O là trung điểm của BC. Lấy D, E thuộc AB , AC sao cho góc DOE = 60 độ
a. Chứng minh tích BD.CE không đổi
b.Tam giác BOD đồng dạng với tam giác OED, OD là phân giác góc BDE
c.Vẽ đường trờn tâm O tiếp xúc với AB . Chứng minh đường tròn này tiếp xúc với DE
Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D và E sao cho góc DOE 60o.a) Chứng minh tích BD.CE không đổi.b) Chứng minh ΔBOD ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.c) Vẽ đường tròn tâm O tiếp xúc với AB. Chứng minh rằng đường tròn này luôn tiếp xúc với DE.
Đọc tiếp
Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D và E sao cho góc DOE = 60o.
a) Chứng minh tích BD.CE không đổi.
b) Chứng minh ΔBOD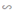 
ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
c) Vẽ đường tròn tâm O tiếp xúc với AB. Chứng minh rằng đường tròn này luôn tiếp xúc với DE.
Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D và E sao cho góc DOE
60
o
.a) Chứng minh tích BD.CE không đổi.b) Chứng minh ΔBOD ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.c) Vẽ đường tròn tâm O tiếp xúc với AB. Chứng minh rằng đường tròn này luôn tiếp xúc với DE.
Đọc tiếp
Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D và E sao cho góc DOE = 60 o .
a) Chứng minh tích BD.CE không đổi.
b) Chứng minh ΔBOD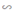 
ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
c) Vẽ đường tròn tâm O tiếp xúc với AB. Chứng minh rằng đường tròn này luôn tiếp xúc với DE.
Bài 1.Cho tam giác ABC có trọng tâm G. Đường thẳng d đi qua G cắt hai cạnh AB và AC. CMR khoảng cách từ A đến d bằng tổng các khoảng cách từ B và C đến d.Bài 2. Cho tam giác ABC cân tại A và đường cao AD. Từ D dựng DE vuông góc AB và DF vuông góc AC (E thuộc AB, F thuộc AC)a) Chứng minh AD là trung trực của đoạn EF.[B]b) [/B]Trên tia đối của tia DE lấy điểm G sao cho DGDE. Chứng minh tam giác CEG vuông.Bài 3. Cho tam giác ABC, vẽ tam giác vuông cân ABD cân tại B,A và D ở hai nửa mặt phẳng đối nh...
Đọc tiếp
Bài 1.Cho tam giác ABC có trọng tâm G. Đường thẳng d đi qua G cắt hai cạnh AB và AC. CMR khoảng cách từ A đến d bằng tổng các khoảng cách từ B và C đến d.
Bài 2. Cho tam giác ABC cân tại A và đường cao AD. Từ D dựng DE vuông góc AB và DF vuông góc AC (E thuộc AB, F thuộc AC)
a) Chứng minh AD là trung trực của đoạn EF.
[B]b) [/B]Trên tia đối của tia DE lấy điểm G sao cho DG=DE. Chứng minh tam giác CEG vuông.
Bài 3. Cho tam giác ABC, vẽ tam giác vuông cân ABD cân tại B,A và D ở hai nửa mặt phẳng đối nhau bờ là đường thẳng BC. Vẽ tam giác vuông cân CBG cân tại B,G và A ở cùng nửa mặt phẳng bờ là đường thẳng BC. Chứng minh rằng GA vuông góc vớ DC.
Bài 4.Cho tam giác ABC trên tia đối của tia BA, CA lần lượt lấy điểm P,Q sao cho BP=CQ. Gọi M,N lần lượt là trung điểm của các đoạn BC,PQ. Đường thẳng MN cắt đường thẩngB,AC theo thứ tự tại B' và C'. Chứng minh rằng tam giác B'AC cân.
Cho tam giác ABC , các điểm E , F thứ tự thuộc các cạnh AC , AB sao cho EF // BC . Lấy P , Q thuộc canh BC sao cho BF < BQ và \(\widehat{PAB}=\widehat{QAC}\) . Gọi M và N thứ tự là hình chiếu vuông góc của C trên QE và B trên PF . Đường tròn ngoại tiếp các tam giác AME và ANF cắt nhau tại R khác A . Chứng minh rằng AR đi qua trung điểm của EF .