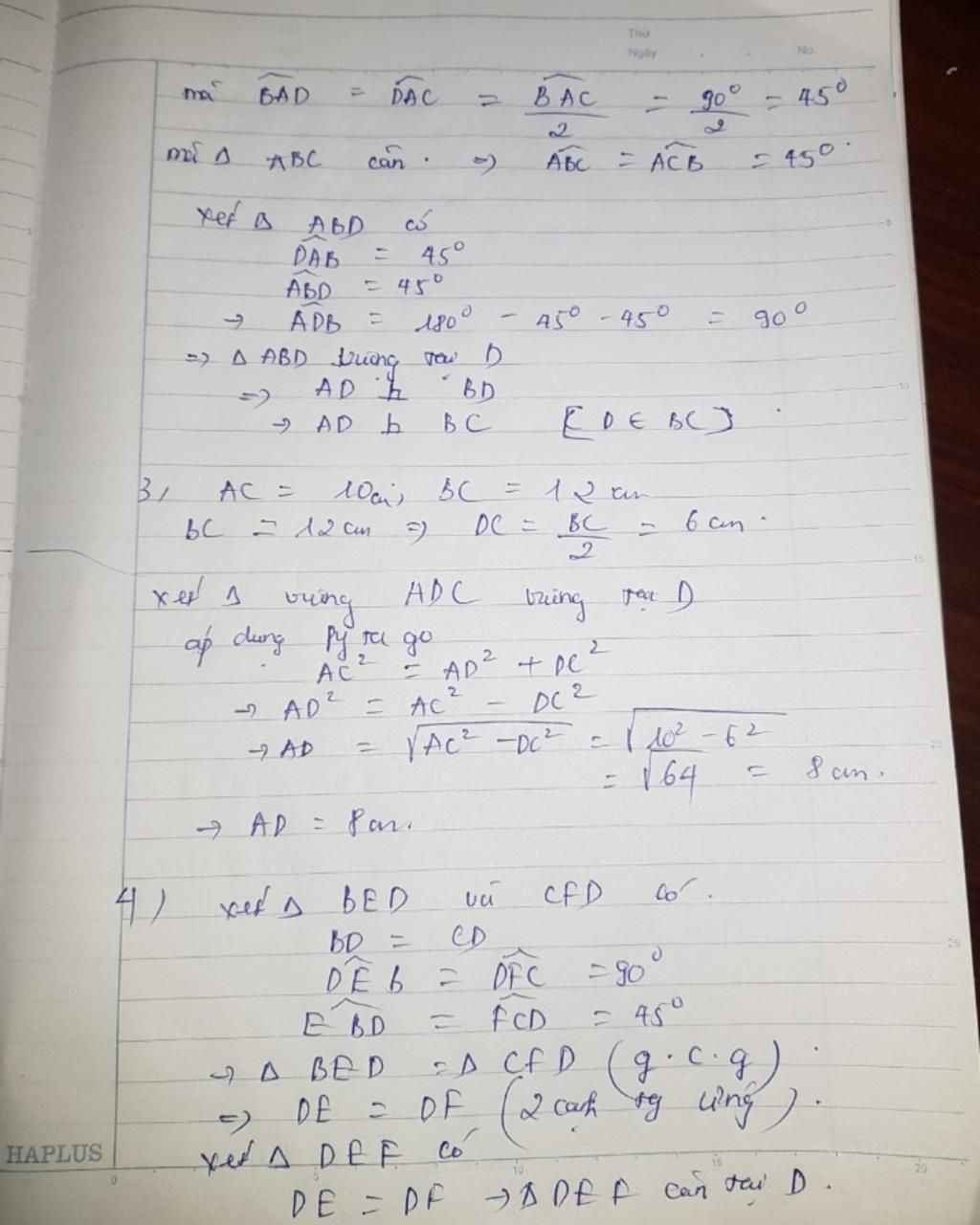a,
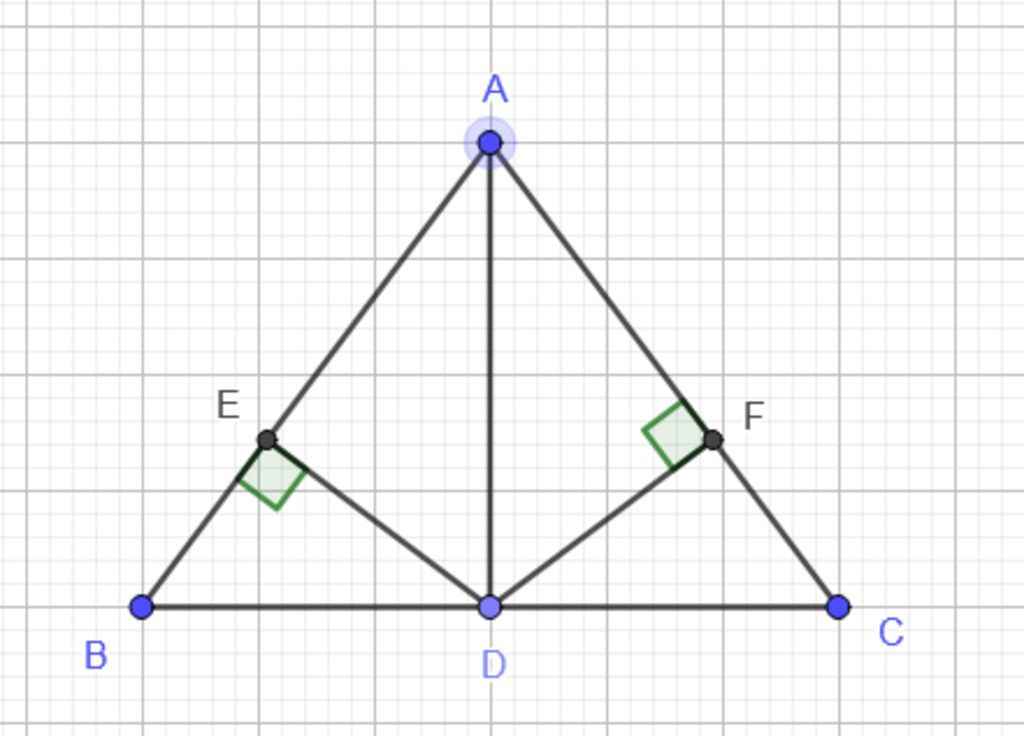
Ta có : D là trung điểm của BC
Mà Δ ABC cân tại A
=> AD là đường cao
=> AD là đường phân giác \(\widehat{BAC}\)
Xét Δ ABD và Δ ACD, có :
\(\widehat{ADB}=\widehat{ADC}=90^o\)
\(\widehat{ABD}=\widehat{ACD}\) (Δ ABC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\) (AD là đường phân giác \(\widehat{BAC}\))
=> Δ ABD = Δ ACD (g.g.g)
b, Ta có : AD là đường cao (cmt)
=> AD ⊥ BC
c, Xét Δ AED và Δ AFD, có :
AD là cạnh chung
\(\widehat{AED}=\widehat{AFD}=90^o\)
\(\widehat{EAD}=\widehat{FAD}\) (AD là đường phân giác \(\widehat{BAC}\))
=> Δ AED = Δ AFD (g.c.g)
=> ED = FD
Xét Δ EBD vuông tại E và Δ FCD vuông tại F, có :
ED = FD
DB = DC (D là trung điểm BC)
=> Δ EBD = Δ FCD (ch - cgv)
d, Ta có : BC = 2DC (D là trung điểm BC)
=>12 = 2DC
=> DC = 6 (cm)
Xét Δ ADC vuông tại D, có :
\(AC^2=AD^2+DC^2\) (định lí Py - ta - go)
=> \(10^2=AD^2+6^2\)
=> \(64=AD^2\)
=> AD = 8 (cm)