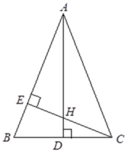
Kẻ đường cao AD. Xét ΔCBE và ΔABD có BEC=ADB=90 B E C ^ = A D B ^ = 90 ∘ và góc B chung nên ΔCBE ~ ΔABD (g.g) => B C A B = B E B D hay 24 A B = 9 12 => AB = 32cm.
Đáp án: B
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho tam giác ABC có AB=16cm; AC=20cm;BC=24cm. Kẻ đường phân giác AI( I ∈ BC ). Hai đường cao BD và CE của tam giác cắt nhau tại H ( H ∈ AC; E ∈ AB)
a) CM Δ ADB ∼ ΔAEC
b) tính IB, IC
c) CM BH*BD+CH*CE=BC2
Cho tam giác ABC cân tại A. Đường thẳng qua C và vuông góc AB tại CE. Tính AB, biết BC = 18cm và BE = 6,75cm.
A. 16cm
B. 32cm
C. 24cm
D. 18cm
Cho tam giác abc cân tại a ab=ac=20cm bc=24cm trên cạnh ab lấy điểm e sao cho ae=af=16cm trên cạnh ac lấy điểm f sao cho ae=à=16cm
a,CM ef song song với bc
b,tính độ dài ei
c, kẻ đường cao ah,bk cắt nhau tại i CM tam giác hbi đồng dạng với tam giác hac
d, tính độ dài ih,bi
Cho tam giác ABC cân tại A, AC = 20cm, BC = 24cm, các đường cao AD và CE cắt nhau ở H. Tính độ dài HD.
A. 12cm
B. 6cm
C. 9cm
D. 10cm
Cho tam giác ABC (AB=AC), AB= 32 cm, BC= 24cm. Đường cao BK
a) Tính CK
b) Hạ AH ⊥ BC, AH cắt BK tại D. Tính DK
c) Lấy E ∈ AB, CE= 24cm. Tính AE
Cho tam giác ABC (AB=AC), AB= 32 cm, BC= 24cm. Đường cao BK
a) Tính CK
b) Hạ AH ⊥ BC, AH cắt BK tại D. Tính DK
c) Lấy E ∈ AB, CE= 24cm. Tính AE
Cho tam giác ABC (AB=AC), AB= 32 cm, BC= 24cm. Đường cao BK
a) Tính CK
b) Hạ AH BC, AH cắt BK tại D. Tính DK
c) Lấy E AB, CE= 24cm. Tính AE
Cho tam giác ABC vuông tại A, biết AB=24cm, AC=18cm. Đường trung trực của BC cắt BC, BA, AC lần lượt ở M, E, D. a) Chứng minh ∆ADB~∆HIB b) Chứng minh IA.BH=IH.BA c) Tính AH
ai giúp mình bài này vs ạ xd
Bài 3: Cho tam giác ABC vuông tại A có AB=18cm; AC=24cm. Gọi D là trung điểm BC. Đường vuông góc với BC tại D cắt AC tại M và cắt tia BA tại E. a) Chứng minh ∆𝐴𝐵𝐶 ~∆𝐷𝐵𝐸 , từ đó suy ra AB.DE = AC.DB b) Tính độ dài DE, BE c) Chứng minh MA.MC = MD.ME d) Chứng minh ∆𝑀𝐴𝐷 ~∆𝑀𝐸�