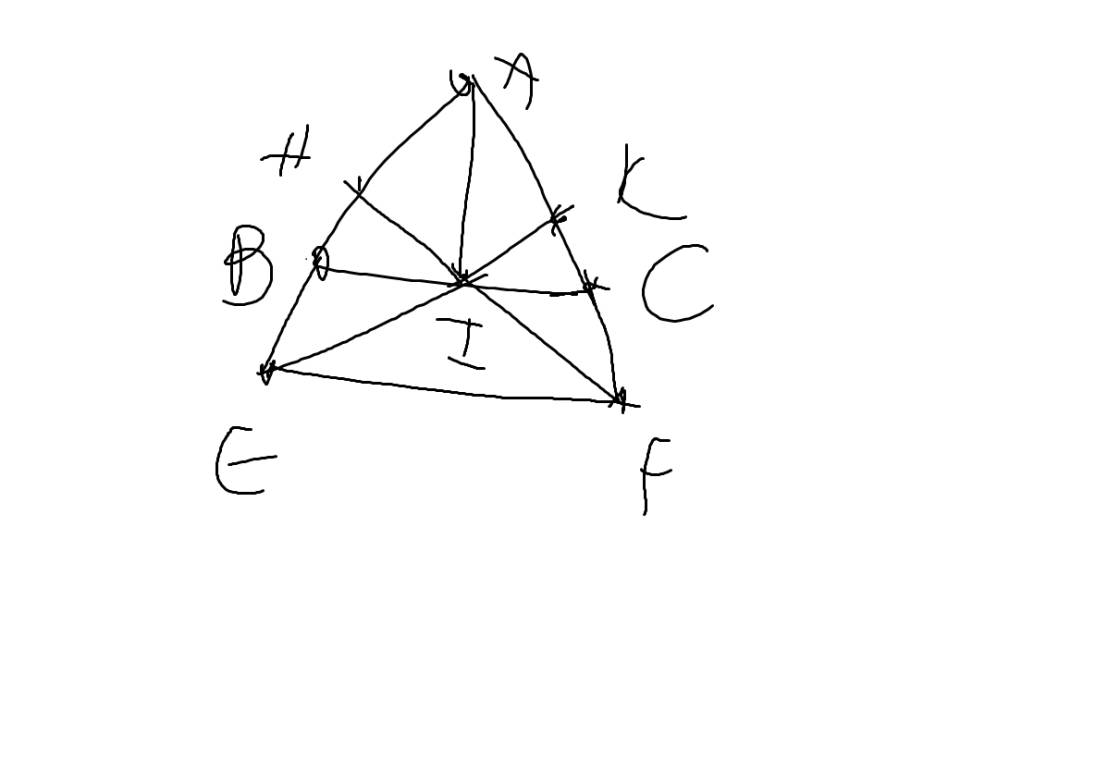
a: Xét ΔIHB vuông tại H và ΔIKC vuông tại K có
IB=IC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔIHB=ΔIKC
b: Ta có: ΔIHB=ΔIKC
=>IB=IC
mà IC>IK(ΔIKC vuông tại K)
nên IB>IK
c:
Ta có: ΔIHB=ΔIKC
=>IH=IK
Xét ΔHIE vuông tại H và ΔKIF vuông tại K có
IH=IK
\(\widehat{HIE}=\widehat{KIF}\)(hai góc đối đỉnh)
Do đó; ΔHIE=ΔKIF
=>HE=KF
Ta có: AH+HB=AB
AK+KC=AC
mà HB=KC và AB=AC
nên AH=AK
Ta có: AH+HE=AE
AK+KF=AF
mà AH=AK và HE=KF
nên AE=AF
=>ΔAEF cân tại A
d: Xét ΔAEF có \(\dfrac{AH}{AE}=\dfrac{AK}{AF}\)
nên HK//EF