Question

. Cho tam giác ABC cân tại A, có AM là đường phân giác của góc A (M∈ BC). Từ M lần lượt kẻ các đường thẳng song song với AB và AC, các đường thẳng này cắt AC tại N, cắt AB tại E.

a) Chứng minh tứ giác AEMN là hình thoi.

b) Gọi D là điểm đối xứng của M qua N. Chứng minh tứ giác ADMB là hình bình hành.

Answer 1

MMỉm đang cần rất gấp  giúp mỉm với

 

Answer 2

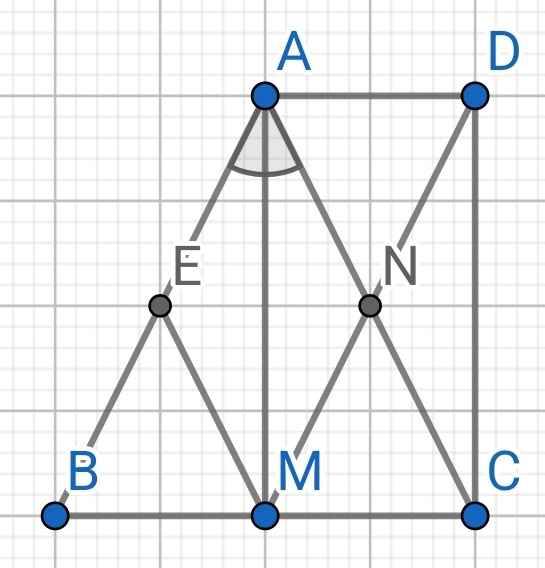  a) Do MN // AB (gt)

⇒ MN // AE

Do ME // AC (gt)

⇒ ME // AN

Do AM là tia phân giác của ∠BAC (gt)

⇒ AM là tia phân giác của ∠EAN

Xét tứ giác AEMN có:

MN // AE (cmt)

ME // AN (cmt)

⇒ AEMN là hình bình hành

Mà AM là tia phân giác của ∠EAN (cmt)

⇒ AEMN là hình thoi

b) Do D là điểm đối xứng của M qua N (gt)

⇒ N là trung điểm của DM

∆ABC cân tại A có AM là tia phân giác của ∠BAC (gt)

⇒ AM cũng là đường trung trực của ∆ABC

⇒ M là trung điểm của BC

∆ABC có:

M là trung điểm của BC (cmt)

MN // AB (gt)

⇒ N là trung điểm của AC

Tứ giác ADCM có:

N là trung điểm của DM (cmt)

N là trung điểm của AC (cmt)

⇒ ADCM là hình bình hành

⇒ AD // CM

⇒ AD // BM

Do MN // AB (gt)

⇒ MD // AB

Tứ giác ADMB có:

MD // AB (cmt)

AD // BM (cmt)

⇒ ADMB là hình bình hành