a: Xet ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
=>ΔABM=ΔACM
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
=>ΔAEF cân tại A
a: Xet ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
=>ΔABM=ΔACM
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
=>ΔAEF cân tại A
Cho tam giác ABC cân tại A, D là trung điểm của BC. Gọi E và F là chân các đường vuông góc kẻ từ D đến AB và AC. Chứng minh rằng DE = DF.
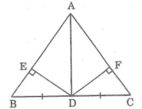
Cho tam giác ABC cân tại A, D là trung điểm của BC. Gọi E và F là chân các đường vuông góc kẻ từ D đến AB và AC. Chứng minh DE = DF
Cho tam giác ABC cân tại A, D là trung điểm của BC. Gọi E và F là chân các đường vuông góc kẻ từ D đến AB và AC. Chứng minh rằng DE = DF.
Cho tam giác ABC cân tại A. Kẻ BD ^ AC, CE ^ AB (D Î AC; E Î AB). Gọi O là giao điểm của BD và CE.
a/ Chứng minh tam giác ADB = D AEC
b/ Chứng minh tam giác BOC cân
c/ Chứng minh ED//BC
d/ Gọi M là trung điểm BC. Chứng minh BC = 2EM.
Bài 1Cho tam giác ABC cân tại A, D là trung điểm của BC, E và F là chân các đường vuông góc kẻ từ D đến AB và AC. Chứng minh DE=DF.
Bài 2 tam giác ABC, E là trung điểm của AC. Qua E kẻ đường thẳng || BC cắt AB ở F. Đường thẳng qua E cắt BC tại D. Chứng minh F là trung điểm của AB và D là trung điểm của BC.
Ai giúp e giải 2 bài này với
Cho tam giác ABC cân tại A ( BAC<90 ). Kẻ BI vuông góc với AC tại I. Trên cạnh BC lấy điểm M bất kì ( M khác B và C). Gọi D, E, F lần lượt là chân đường vuông góc kẻ từ M đến AB, AC, BI.
a) Chứng minh ![]() .
.
b) Cho BC=10, CI=. Tính MD+ME.
c) Trên tia đối của tia CA lấy K sao cho CK=EI. Chứng minh BC đi qua trung điểm của DK.
Cho tam giác ABC cân tại A. Lấy M thuộc cạnh AB và N thuộc cạnh AC sao cho AM=AN.
a) Chứng minh rằng tam giác AMN cân
b) Chứng minh MN//BC
c) Gọi I là giao điểm của CM và BN. Chứng minh 2 tam giác BIC và MIN cân
d) Gọi E là trung điểm MN, F là trung điểm BC. Chứng minh A,E,F,I thẳng hàng
Bài 4: (3,5điểm): Cho tam giác ABC cân tại A, AM là đường phân giác (M thuộc BC).
a) Chứng minh: tam giác ABM = tam giác ACM.
b) Gọi I là trung điểm của cạnh AC, trên tia đối của tia IM lấy điểm E sao cho IE=IM. Chứng minh: AM = EC.
c) Qua M kẻ đường thẳng song song với AC, đường thẳng này cắt tia EC tại K.
Chứng minh: MC là tia phân giác của góc EMK
d) Gọi H là giao điểm của MC và KI, tia EH cắt MK tại F. Biết AM=3cm, chứng minh: chu vi tam giác MIF lớn hơn 6cm
giúp mình vs
Cho tg nhọn ABC cân tại A, đường cao BH, trung tuyến AM
a)Cm AM là đường phân giác
b)Từ M kẻ MD⊥AB, ME⊥AC, MF⊥BH.(D ∈AB, E ∈AC, F ∈BH). Chứng minh rằngME=FH
c) Gọi K là giao điểm của AM và BH. Chứng minh CK//MD