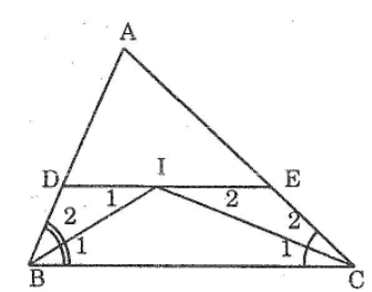
Ta có hình vẽ:
Ta có: BI là pg góc B
=> góc DBI = góc IBC
Mà góc DIB = góc IBC (DE // BC)
=> góc DBI = góc DIB
=> tam giác BDI cân
=> BD = DI
Ta có: CI là phân giác góc C
=> góc ECI = góc ICB
Mà góc EIC = góc ICB (DE // BC)
=> góc ECI = góc EIC
=> tam giác CEI cân
=> CE = IE
Ta có: BD = DI; CE = IE
=> BD + CE = DI + IE
hay BD + CE = DE
hay DE = BD + CE
Ta có: DI // BC (gt)
Suy ra:∠I1 =∠B1(so le trong) (1)
Lại có:∠B1 =∠B2 (2)
(vì BI là yia phân giác góc B)
Từ (1) và (2) suy ra:∠I1 =∠B2
=>∆BDI cân tại D =>BD=DI (3)
Mà IE // BC (gt) =>∠I1 =∠C1 (so le trong) (4)
Đồng thời: ∠C1=∠C2 (vì CI là phân giác của góc C) (5)
Từ (4) và (5) suy ra: ∠C1=∠C2. Suy ra. ∠CEI cân tại E
Suy ra: CE = EI (hai cạnh tương ứng) (6)
Từ (3) và (6) suy ra: BD + CE = DI + EI = DE